What Is 2.375 As A Fraction
News Co
May 08, 2025 · 5 min read
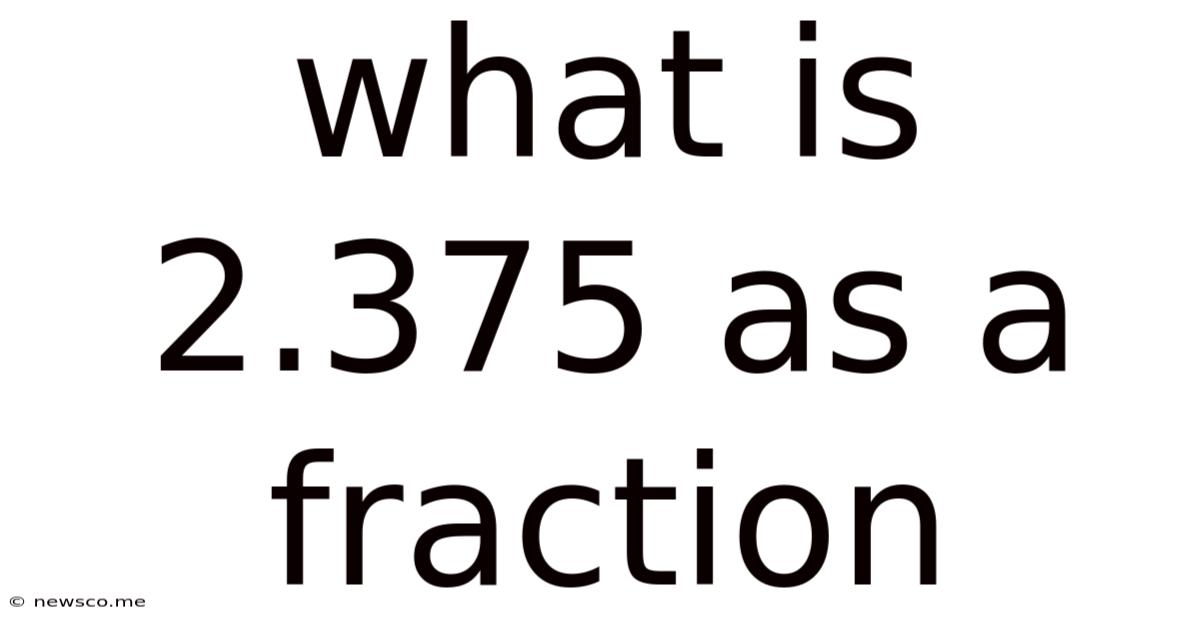
Table of Contents
What is 2.375 as a Fraction? A Comprehensive Guide
Converting decimals to fractions might seem daunting at first, but with a structured approach, it becomes a straightforward process. This comprehensive guide will walk you through the steps of converting the decimal 2.375 into a fraction, explaining the underlying principles and offering helpful tips for similar conversions. We'll also explore the broader context of decimal-to-fraction conversions and their applications in various fields.
Understanding Decimals and Fractions
Before diving into the conversion, let's refresh our understanding of decimals and fractions. A decimal represents a number using a base-ten system, where the digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. A fraction, on the other hand, represents a part of a whole, expressed as a ratio of two integers: a numerator (top number) and a denominator (bottom number).
For example, 0.5 is a decimal representing half (1/2) and 0.25 represents a quarter (1/4). The decimal system and the fractional system are two different ways to represent the same numerical values.
Converting 2.375 to a Fraction: A Step-by-Step Approach
The conversion of 2.375 to a fraction involves several key steps:
Step 1: Identify the Place Value of the Last Digit
The last digit in 2.375 is 5, which is in the thousandths place. This means our denominator will be 1000 (10 to the power of 3, as there are three digits after the decimal point).
Step 2: Express the Decimal as a Fraction
We can express 2.375 as the fraction 2375/1000. This is a straightforward representation based on the place value identified in Step 1.
Step 3: Simplify the Fraction
The fraction 2375/1000 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both 2375 and 1000 without leaving a remainder.
Finding the GCD can be done through various methods, including:
- Prime Factorization: Break down both numbers into their prime factors and identify the common factors.
- Euclidean Algorithm: A more efficient method for larger numbers, involving repeated division until the remainder is zero.
Let's use prime factorization:
- 2375 = 5³ x 19
- 1000 = 2³ x 5³
The greatest common divisor is 5³, which is 125.
Step 4: Divide Both Numerator and Denominator by the GCD
Dividing both the numerator (2375) and the denominator (1000) by 125, we get:
2375 ÷ 125 = 19 1000 ÷ 125 = 8
Therefore, the simplified fraction is 19/8.
Step 5: Convert to a Mixed Number (Optional)
The fraction 19/8 is an improper fraction (where the numerator is larger than the denominator). We can convert it to a mixed number, which consists of a whole number and a proper fraction.
To do this, divide the numerator (19) by the denominator (8):
19 ÷ 8 = 2 with a remainder of 3.
So, 19/8 can be expressed as the mixed number 2 3/8. This confirms our initial decimal of 2.375, representing 2 whole units and 3/8 of another unit.
Understanding the Underlying Mathematics
The process of converting decimals to fractions relies on the fundamental relationship between the decimal system and fractions. The decimal point separates the whole number part from the fractional part. Each digit to the right of the decimal point represents a power of 10 in the denominator. For instance:
- 0.1 = 1/10
- 0.01 = 1/100
- 0.001 = 1/1000
Therefore, by understanding the place value of each digit, you can directly translate the decimal into a fraction and then simplify as necessary.
Practical Applications of Decimal-to-Fraction Conversions
The ability to convert decimals to fractions is crucial in various fields:
-
Engineering and Physics: Many calculations in these fields require precise representations, and fractions often provide a more accurate representation than decimals, particularly when dealing with ratios and proportions.
-
Cooking and Baking: Recipes often use fractions to indicate ingredient amounts, requiring accurate conversions for consistent results.
-
Finance: Calculations involving interest rates, percentages, and stock prices frequently involve fractions and decimals.
-
Mathematics: Understanding decimal-to-fraction conversion is essential for various mathematical operations, including adding, subtracting, multiplying, and dividing fractions and decimals.
Handling More Complex Decimal Conversions
The method explained above can be extended to handle more complex decimals, even those with repeating or non-terminating digits. However, these conversions might require more advanced techniques, such as using continued fractions or infinite series.
For instance, converting a repeating decimal like 0.333... (which represents 1/3) requires understanding the concept of geometric series.
Tips for Accurate Decimal-to-Fraction Conversions
-
Double-check your work: Carefully verify each step to ensure accuracy.
-
Use a calculator (if permitted): Calculators can aid in finding the greatest common divisor (GCD) and simplifying fractions.
-
Practice regularly: The more you practice, the more comfortable and proficient you'll become.
-
Learn different simplification techniques: Familiarize yourself with various methods for finding the GCD, such as prime factorization and the Euclidean algorithm.
Conclusion
Converting 2.375 to a fraction involves expressing the decimal as a fraction with a denominator based on the place value of the last digit, simplifying the fraction by finding the GCD of the numerator and denominator, and optionally converting the result to a mixed number. This process relies on the fundamental connection between decimals and fractions and has applications in numerous fields. Mastering this conversion enhances mathematical skills and opens doors to problem-solving in various contexts. Remember to practice regularly and utilize different simplification techniques for enhanced accuracy and efficiency.
Latest Posts
Latest Posts
-
The Cube Of The Product Of 4 And A Number
May 08, 2025
-
Altitude To The Base Of An Isosceles Triangle
May 08, 2025
-
Which Of These Relations Are Functions
May 08, 2025
-
What Is The Minimum Eccentricity An Ellipse Can Have
May 08, 2025
-
1 1 3 Plus 1 1 3
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 2.375 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.