What Is 4 To The 2 Power
News Co
Apr 05, 2025 · 5 min read
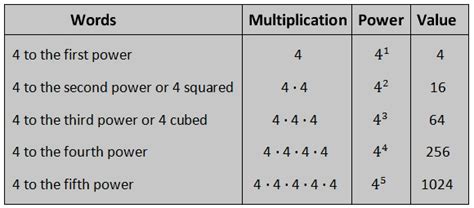
Table of Contents
What is 4 to the 2nd Power? A Deep Dive into Exponents and Their Applications
The seemingly simple question, "What is 4 to the 2nd power?" opens a door to a vast world of mathematical concepts. While the answer itself is straightforward (16), understanding the underlying principles of exponents and their diverse applications unlocks a deeper appreciation of mathematics and its relevance to various fields. This comprehensive guide will not only answer the initial question but will delve into the intricacies of exponents, their properties, and their far-reaching implications.
Understanding Exponents: The Power of Repeated Multiplication
At its core, an exponent represents repeated multiplication. In the expression 4², the '4' is called the base, and the '2' is called the exponent or power. This notation signifies that the base (4) is multiplied by itself the number of times indicated by the exponent (2). Therefore, 4² = 4 x 4 = 16.
Let's break this down further:
- Base: The number being multiplied repeatedly. In our example, the base is 4.
- Exponent: The number indicating how many times the base is multiplied by itself. In our example, the exponent is 2.
- Result: The product obtained after performing the repeated multiplication. In our example, the result is 16.
Expanding the Concept: Beyond 4²
Understanding the fundamental principle allows us to tackle more complex exponents. For example:
- 4³ (4 to the power of 3): This means 4 x 4 x 4 = 64
- 4⁴ (4 to the power of 4): This means 4 x 4 x 4 x 4 = 256
- 4⁵ (4 to the power of 5): This means 4 x 4 x 4 x 4 x 4 = 1024
And so on. The pattern is clear: as the exponent increases, the result grows exponentially. This exponential growth is a key characteristic that underlies many phenomena in the natural world and various applications in different fields.
Properties of Exponents: Rules to Simplify Calculations
Working with exponents becomes much more efficient when we understand their properties. These properties allow us to simplify complex expressions and solve equations more effectively. Here are some crucial exponent properties:
-
Product of Powers: When multiplying two numbers with the same base, you add the exponents. For example: 4² x 4³ = 4⁽²⁺³⁾ = 4⁵ = 1024
-
Quotient of Powers: When dividing two numbers with the same base, you subtract the exponents. For example: 4⁵ / 4² = 4⁽⁵⁻²⁾ = 4³ = 64
-
Power of a Power: When raising a power to another power, you multiply the exponents. For example: (4²)³ = 4⁽²ˣ³⁾ = 4⁶ = 4096
-
Power of a Product: When raising a product to a power, you raise each factor to that power. For example: (2 x 4)² = 2² x 4² = 4 x 16 = 64
-
Power of a Quotient: When raising a quotient to a power, you raise both the numerator and the denominator to that power. For example: (4/2)² = 4²/2² = 16/4 = 4
-
Zero Exponent: Any non-zero number raised to the power of zero is equal to 1. For example: 4⁰ = 1
-
Negative Exponent: A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example: 4⁻² = 1/4² = 1/16
Practical Applications of Exponents: Where We See Them in Action
The concept of exponents transcends the realm of abstract mathematics and finds practical applications in various fields:
1. Science and Engineering:
-
Compound Interest: The power of exponential growth is vividly demonstrated in compound interest calculations. The formula for compound interest involves exponents to determine the future value of an investment.
-
Exponential Decay: Radioactive decay, the process by which unstable atomic nuclei lose energy by emitting radiation, follows an exponential decay pattern. Exponents are crucial for modeling and predicting the decay rate.
-
Population Growth: The growth of populations, whether it be bacteria, animals, or humans, can often be modeled using exponential functions. Exponents allow us to project future population sizes.
-
Physics: Exponents are extensively used in various physics formulas, including those describing motion, energy, and electromagnetism. Newton's Law of Universal Gravitation, for instance, incorporates exponents to quantify the force of gravity.
2. Computer Science:
-
Big O Notation: In computer science, Big O notation uses exponents to express the time complexity and space complexity of algorithms. This notation helps programmers assess the efficiency of their algorithms.
-
Binary Numbers: The binary number system, the foundation of digital computation, relies on powers of 2. Each digit in a binary number represents a power of 2, allowing for the efficient representation and manipulation of data.
3. Finance:
- Present Value and Future Value Calculations: Exponents are integral to calculating the present value and future value of investments, helping individuals and businesses make informed financial decisions.
4. Biology:
- Cellular Growth and Division: The growth and division of cells in living organisms are often exponential processes. Exponents help in modeling and understanding the rate of cell proliferation.
Beyond the Basics: Exploring More Complex Exponents
While we've focused primarily on integer exponents, the concept extends to fractional exponents, irrational exponents, and even complex exponents.
Fractional Exponents: Roots and Radicals
Fractional exponents represent roots. For example, 4^(1/2) is the square root of 4, which is 2. Similarly, 4^(1/3) is the cube root of 4, and so on. A fractional exponent of the form a/b means the b-th root of the number raised to the power of a.
Irrational Exponents: Introducing e and Natural Logarithms
Irrational exponents, such as 4^π (4 raised to the power of pi), might seem unusual, but they are perfectly valid and arise in various mathematical contexts. These exponents are often connected to the concept of the natural logarithm (ln) and the mathematical constant e (approximately 2.718).
Conclusion: The Enduring Importance of Exponents
The seemingly simple question of "What is 4 to the 2nd power?" leads us on a journey through the world of exponents, revealing their fundamental importance in mathematics and their widespread applications in various fields. From understanding compound interest to modeling radioactive decay, from analyzing algorithms to studying cellular growth, exponents provide a powerful tool for understanding and quantifying phenomena in the world around us. Mastering the concepts of exponents and their properties unlocks a deeper appreciation of mathematics and its role in solving real-world problems. The seemingly simple 16 is, therefore, a gateway to a vast and fascinating mathematical landscape.
Latest Posts
Latest Posts
-
Is A Kite Always A Quadrilateral
Apr 06, 2025
-
What Is One Percent Of 1000
Apr 06, 2025
-
How Many Inches In 21 Cm
Apr 06, 2025
-
What Is The Percent Of 1 5
Apr 06, 2025
-
Convert 16 Degrees C To Fahrenheit
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The 2 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
