What Is The Decimal Form Of 5/9
News Co
May 08, 2025 · 5 min read
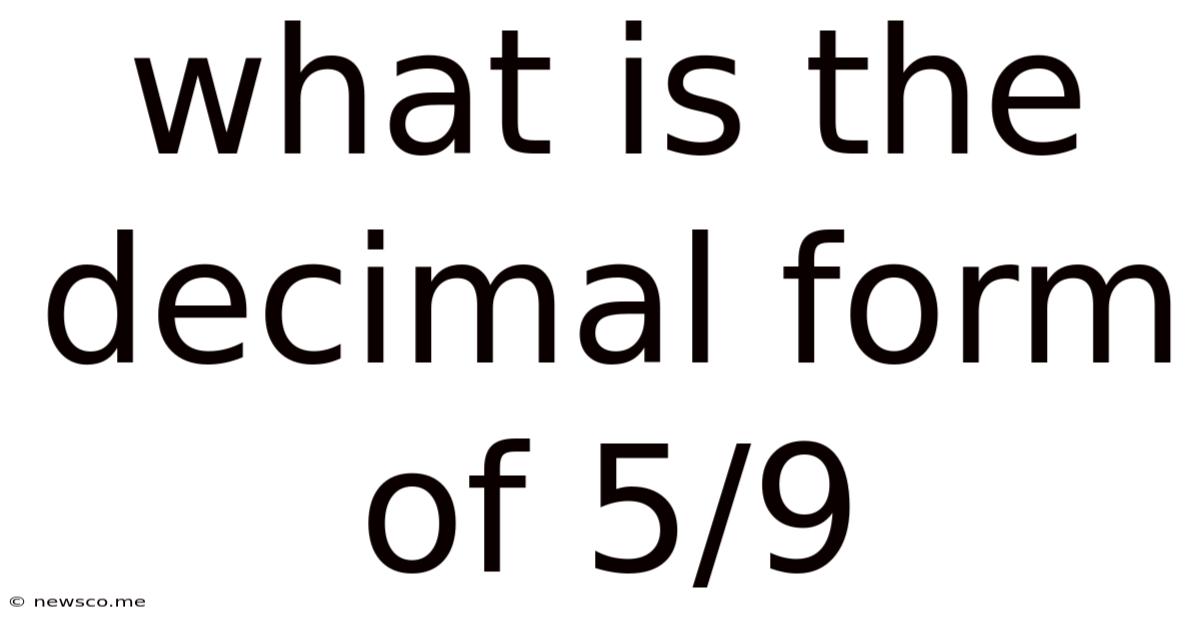
Table of Contents
What is the Decimal Form of 5/9? A Deep Dive into Fractions and Decimal Conversions
The seemingly simple question, "What is the decimal form of 5/9?" opens a door to a fascinating world of mathematical concepts. While a quick calculation might provide the answer, exploring the why behind the conversion reveals fundamental principles of fractions, decimals, and their interrelationship. This article will delve deep into this seemingly basic problem, uncovering the underlying mechanics and exploring related mathematical ideas.
Understanding Fractions and Decimals
Before tackling the conversion of 5/9, let's establish a solid foundation in understanding fractions and decimals.
Fractions: Representing Parts of a Whole
A fraction represents a part of a whole. It consists of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 5/9, 5 is the numerator and 9 is the denominator. This means we have 5 out of 9 equal parts of a whole.
Decimals: Another Way to Represent Parts of a Whole
Decimals are another way to represent parts of a whole. They use a base-ten system, where each place value to the right of the decimal point represents a decreasing power of 10 (tenths, hundredths, thousandths, and so on). For instance, 0.5 represents five-tenths, and 0.25 represents twenty-five hundredths.
The Interplay Between Fractions and Decimals
Fractions and decimals are essentially two different ways of expressing the same thing – parts of a whole. Converting between them is a crucial skill in mathematics. The process involves finding an equivalent representation of the same value using a different notation.
Converting 5/9 to Decimal Form: The Long Division Method
The most straightforward method for converting a fraction to a decimal is through long division. We divide the numerator (5) by the denominator (9):
0.555...
9 | 5.000
-4.5
0.50
-0.45
0.050
-0.045
0.005...
As you can see, the division process continues indefinitely, resulting in a repeating decimal: 0.555... The ellipsis (...) indicates that the digit 5 repeats infinitely. This type of decimal is called a repeating decimal or a recurring decimal.
Representing Repeating Decimals
There are a couple of ways to represent a repeating decimal concisely:
-
Using a bar: A bar is placed over the repeating digits. In this case, we write 0.5̅ to indicate that the digit 5 repeats indefinitely.
-
Using ellipsis: As shown in the long division example, the ellipsis (...) indicates that the pattern continues infinitely.
Both methods effectively convey the same information – an infinitely repeating sequence of the digit 5.
Why does 5/9 result in a repeating decimal?
The reason 5/9 results in a repeating decimal lies in the nature of the denominator. When the denominator of a fraction has prime factors other than 2 and 5 (the prime factors of 10), the decimal representation will be a repeating decimal. Since 9 is 3 x 3, it contains a prime factor other than 2 and 5, leading to the repeating decimal.
Other Methods for Converting Fractions to Decimals
While long division is the most fundamental method, other techniques can be used, especially for simpler fractions.
Using Equivalent Fractions
Sometimes, you can create an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). This makes direct conversion to a decimal simple. However, this method isn't applicable to 5/9 because there's no whole number you can multiply 9 by to get a power of 10.
Using a Calculator
Calculators provide a quick and easy way to convert fractions to decimals. Simply enter 5 ÷ 9, and the calculator will display 0.555... or a similar representation of the repeating decimal. While convenient, understanding the underlying mathematical principles remains crucial.
Exploring Related Concepts: Terminating and Non-Terminating Decimals
Decimal representations of fractions can be categorized as either terminating or non-terminating.
Terminating Decimals
A terminating decimal has a finite number of digits after the decimal point. For example, 1/2 = 0.5, 1/4 = 0.25, and 1/8 = 0.125 are all terminating decimals. These fractions have denominators whose only prime factors are 2 and/or 5.
Non-Terminating Decimals
A non-terminating decimal has an infinite number of digits after the decimal point. These can be further divided into:
-
Repeating decimals (recurring decimals): As we've seen with 5/9, these decimals have a repeating pattern of digits.
-
Non-repeating decimals (irrational numbers): These decimals have an infinite number of digits without any repeating pattern. Examples include π (pi) and √2 (the square root of 2).
The Significance of Repeating Decimals in Mathematics
Repeating decimals are not simply an oddity; they have significant implications in various mathematical fields, including:
-
Number Theory: The study of repeating decimals helps in understanding the properties of rational and irrational numbers and their relationships.
-
Calculus: Repeating decimals play a role in limit calculations and series expansions.
-
Computer Science: Representing and manipulating repeating decimals efficiently is a concern in computer programming, especially when dealing with numerical computations.
Practical Applications of Decimal Conversions
The ability to convert fractions to decimals is vital in numerous practical applications:
-
Engineering and Science: Precision in measurements and calculations often requires decimal representations.
-
Finance: Calculating percentages, interest rates, and other financial metrics relies heavily on decimal conversions.
-
Everyday Life: Dealing with measurements (like inches or centimeters), splitting bills, or calculating discounts all involve the use of decimals.
Conclusion: Beyond the Simple Answer
While the decimal form of 5/9 is simply 0.5̅, the journey to arrive at that answer reveals a wealth of mathematical concepts. Understanding fractions, decimals, long division, and the nature of repeating decimals is crucial for a strong foundation in mathematics. The seemingly simple problem of converting 5/9 to its decimal equivalent serves as a gateway to a deeper appreciation of the fascinating world of numbers and their representations. This knowledge is not just confined to academic pursuits but is practically applicable in diverse fields, highlighting the importance of mastering this fundamental mathematical skill.
Latest Posts
Latest Posts
-
Which Of The Following Is Not A Polynomial Identity
May 08, 2025
-
12 5 Percent As A Fraction In Simplest Form
May 08, 2025
-
What Is 17 Pounds In Dollars
May 08, 2025
-
Convert 70 British Pounds To Dollars
May 08, 2025
-
Exactly One Pair Of Opposite Sides Are Parallel
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Decimal Form Of 5/9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.