What Is The Lcm Of 14 And 12
News Co
Apr 07, 2025 · 5 min read
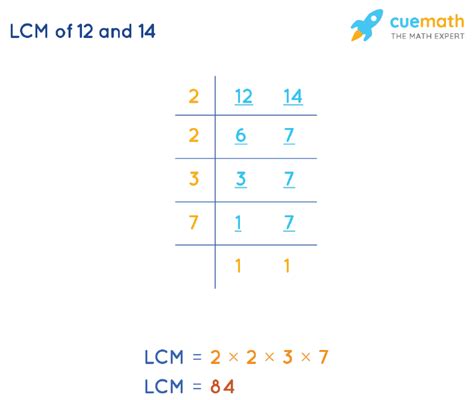
Table of Contents
What is the LCM of 14 and 12? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it provides a valuable foundation in mathematics and problem-solving. This article will explore what the LCM of 14 and 12 is, delve into multiple methods for finding the LCM, and expand on its applications beyond basic arithmetic.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 14 and 12, let's define what a least common multiple actually is. The LCM of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly.
For example, let's consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16... Multiples of 3 are 3, 6, 9, 12, 15, 18... The smallest number that appears in both lists is 6. Therefore, the LCM of 2 and 3 is 6.
This concept is crucial in various mathematical contexts, including simplifying fractions, solving problems related to cycles and patterns, and even in more advanced areas like abstract algebra.
Methods for Finding the LCM of 14 and 12
There are several methods to determine the LCM of two numbers. We'll explore three common approaches: listing multiples, prime factorization, and using the greatest common divisor (GCD).
1. Listing Multiples
The most straightforward method, though often less efficient for larger numbers, involves listing the multiples of each number until a common multiple is found.
- Multiples of 14: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144...
By comparing the lists, we observe that the smallest common multiple is 84. Therefore, the LCM of 14 and 12 is 84. This method is easily understood but becomes cumbersome with larger numbers.
2. Prime Factorization
Prime factorization involves breaking down each number into its prime factors (numbers divisible only by 1 and themselves). This method is more efficient than listing multiples, especially when dealing with larger numbers.
- Prime factorization of 14: 2 x 7
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
To find the LCM using prime factorization, we take the highest power of each prime factor present in either factorization and multiply them together:
2² x 3 x 7 = 4 x 3 x 7 = 84
Therefore, the LCM of 14 and 12 is 84 using the prime factorization method. This method provides a more systematic and efficient way to find the LCM, especially for larger numbers.
3. Using the Greatest Common Divisor (GCD)
The GCD (Greatest Common Divisor) is the largest number that divides both numbers without leaving a remainder. There's a useful relationship between the LCM and GCD of two numbers:
LCM(a, b) x GCD(a, b) = a x b
First, let's find the GCD of 14 and 12 using the Euclidean algorithm:
- Divide the larger number (14) by the smaller number (12): 14 = 12 x 1 + 2
- Replace the larger number with the smaller number (12) and the smaller number with the remainder (2): 12 = 2 x 6 + 0
- The GCD is the last non-zero remainder, which is 2.
Now, we can use the formula:
LCM(14, 12) x GCD(14, 12) = 14 x 12 LCM(14, 12) x 2 = 168 LCM(14, 12) = 168 / 2 = 84
Therefore, the LCM of 14 and 12 is 84 using the GCD method. This method is particularly useful when dealing with larger numbers where finding prime factors can be time-consuming.
Applications of LCM
The concept of LCM extends far beyond simple arithmetic exercises. It has practical applications in various fields:
1. Scheduling and Cyclical Events
Imagine two buses that arrive at a bus stop on different schedules. One bus arrives every 12 minutes, and the other arrives every 14 minutes. To find out when both buses will arrive at the same time, you need to find the LCM of 12 and 14. The LCM (84) represents the time in minutes when both buses will arrive simultaneously.
2. Fraction Addition and Subtraction
When adding or subtracting fractions with different denominators, finding the LCM of the denominators is essential to find a common denominator. This allows for easy addition or subtraction of the fractions.
3. Gear Ratios and Mechanical Systems
In engineering and mechanics, LCM is used in calculations involving gear ratios and other cyclical mechanical systems. Understanding the LCM helps in determining the synchronization of moving parts.
4. Music Theory
In music theory, LCM is used to determine the least common multiple of different note durations or rhythmic patterns. This helps in creating harmonious and rhythmically consistent musical compositions.
5. Computer Science
LCM finds application in various computer science algorithms and processes, particularly in areas involving synchronization and scheduling.
Beyond the Basics: LCM and More Complex Scenarios
While we've focused on finding the LCM of two numbers, the concept extends to finding the LCM of three or more numbers. The methods discussed – prime factorization and the GCD-based approach – can be adapted for multiple numbers. For example, to find the LCM of 12, 14, and 21:
-
Prime Factorization:
- 12 = 2² x 3
- 14 = 2 x 7
- 21 = 3 x 7
The LCM is 2² x 3 x 7 = 84.
-
Using GCD (iterative approach): You would find the GCD of any two numbers, then find the GCD of the result and the remaining number, and so on. This process becomes more complex with a larger number of inputs but is still an effective method.
Conclusion: Mastering the LCM
Understanding the least common multiple is crucial for a strong foundation in mathematics. Knowing how to calculate the LCM using different methods – listing multiples, prime factorization, and the GCD approach – equips you with versatile problem-solving skills. The applications of LCM extend beyond basic arithmetic, finding relevance in various fields, highlighting its importance in practical applications and theoretical understanding. From scheduling to music composition, the concept of LCM plays a significant role in our world. By mastering the LCM, you're not just learning a mathematical concept, but you're acquiring a powerful tool applicable across diverse disciplines.
Latest Posts
Latest Posts
-
12 7 As A Mixed Number
Apr 08, 2025
-
2 5 8 Inches In Decimals
Apr 08, 2025
-
Find An Nth Degree Polynomial Function
Apr 08, 2025
-
Common Factors Of 8 And 16
Apr 08, 2025
-
What Is Square Root Of 58
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 14 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.