What Is The Square Root Of 105
News Co
Apr 05, 2025 · 5 min read
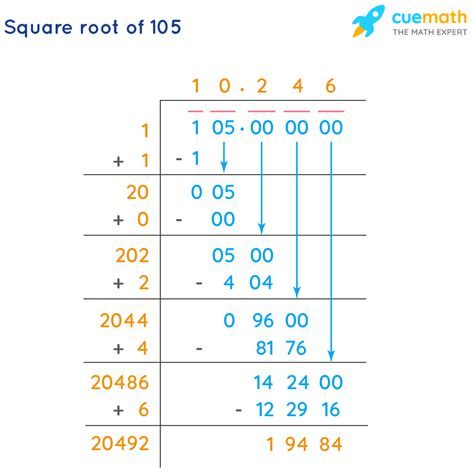
Table of Contents
What is the Square Root of 105? A Deep Dive into Square Roots and Approximation Techniques
The question, "What is the square root of 105?" might seem simple at first glance. However, delving into its answer reveals a fascinating journey into the world of mathematics, exploring different methods of approximation and the nuances of irrational numbers. 105 isn't a perfect square (a number that results from squaring an integer), meaning its square root isn't a whole number. This necessitates the use of various techniques to find an approximate value. Let's embark on this journey together.
Understanding Square Roots
Before we tackle the square root of 105 specifically, let's establish a foundational understanding of what a square root is. The square root of a number is a value that, when multiplied by itself (squared), equals the original number. For example:
- The square root of 9 is 3, because 3 * 3 = 9.
- The square root of 16 is 4, because 4 * 4 = 16.
Mathematically, the square root of a number 'x' is denoted as √x or x<sup>1/2</sup>.
Why 105 Isn't a Perfect Square
A perfect square is the result of multiplying an integer by itself. Let's examine the integers around 105:
- 10<sup>2</sup> = 100
- 11<sup>2</sup> = 121
Since 105 falls between 100 and 121, its square root lies between 10 and 11. This confirms that the square root of 105 is an irrational number, meaning it cannot be expressed as a simple fraction and its decimal representation goes on forever without repeating.
Methods for Approximating the Square Root of 105
Several methods can be employed to approximate the square root of 105. Let's explore some of the most common:
1. Using a Calculator
The simplest and most direct method is using a calculator. Most calculators have a square root function (√). Inputting 105 will yield an approximation such as 10.24695. While convenient, this method doesn't provide insight into the underlying mathematical principles.
2. The Babylonian Method (or Heron's Method)
This iterative method provides increasingly accurate approximations with each iteration. It starts with an initial guess and refines it through successive calculations:
-
Initial Guess: Let's start with an initial guess of 10 (since 10<sup>2</sup> = 100 is close to 105).
-
Iteration 1: Divide 105 by the initial guess: 105 / 10 = 10.5. Then, average the result with the initial guess: (10 + 10.5) / 2 = 10.25.
-
Iteration 2: Repeat the process using the new approximation (10.25): 105 / 10.25 ≈ 10.2439. Average this with 10.25: (10.25 + 10.2439) / 2 ≈ 10.24695.
-
Further Iterations: Continue this process for more accurate results. Each iteration brings the approximation closer to the true value.
The Babylonian method showcases a practical approach to finding increasingly accurate approximations. The more iterations you perform, the closer you'll get to the actual value.
3. Linear Approximation
This method utilizes the tangent line to the square root function at a nearby point to estimate the square root. While less precise than the Babylonian method, it’s conceptually simpler.
Let's use the point (100, 10) which is close to 105. The derivative of f(x) = √x is f'(x) = 1/(2√x). At x = 100, f'(100) = 1/20. The equation of the tangent line is:
y - 10 = (1/20)(x - 100)
Substituting x = 105:
y - 10 = (1/20)(105 - 100) = 0.25
y = 10.25
This method gives a quick, albeit less precise, approximation of 10.25.
4. Using the Binomial Theorem
The binomial theorem allows us to approximate the square root of a number close to a perfect square. Since 105 is close to 100, we can use the binomial theorem to approximate √105:
√105 = √(100 + 5) = 10√(1 + 5/100)
Using the binomial approximation (1 + x)<sup>n</sup> ≈ 1 + nx for small x:
√105 ≈ 10(1 + (1/2)(5/100)) = 10(1 + 0.025) = 10.25
This method also provides a reasonably quick approximation of 10.25.
Understanding the Limitations of Approximations
It's crucial to acknowledge that all the methods above provide approximations, not exact values. The square root of 105 is an irrational number, meaning its decimal representation is infinite and non-repeating. The accuracy of the approximation depends on the chosen method and the number of iterations (for iterative methods). The calculator provides a more precise approximation than the other methods outlined here, but even that is a truncated representation of the true, infinitely long decimal.
Practical Applications of Square Roots
Understanding square roots extends beyond theoretical mathematics; they have numerous practical applications in various fields:
- Physics: Calculating velocity, acceleration, and distance.
- Engineering: Designing structures, calculating forces, and determining stability.
- Computer Graphics: Rendering images and animations, calculating distances and transformations.
- Finance: Calculating investment returns and compound interest.
- Statistics: Calculating standard deviations and variances.
Conclusion
The seemingly simple question, "What is the square root of 105?", opens a window into the fascinating world of square roots, irrational numbers, and approximation techniques. While we cannot express the square root of 105 as a finite decimal, various methods allow us to approximate its value with increasing accuracy. Understanding these methods and their limitations provides a deeper appreciation for the power and subtlety of mathematics. From simple calculator usage to sophisticated iterative methods like the Babylonian method and leveraging the binomial theorem or linear approximation, different approaches offer varying levels of precision. The choice of method depends on the desired level of accuracy and the computational resources available. Ultimately, the pursuit of the square root of 105 serves as a valuable exercise in mathematical exploration and problem-solving.
Latest Posts
Latest Posts
-
Round Answer To 2 Decimal Places
Apr 06, 2025
-
Which Is Larger 3 4 Or 7 8
Apr 06, 2025
-
150 Square Meters To Square Feet
Apr 06, 2025
-
What Is An Equivalent Fraction For 4 5
Apr 06, 2025
-
1 Tenth Of A Mile In Feet
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 105 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
