What Is The Square Root Of 149
News Co
Apr 05, 2025 · 5 min read
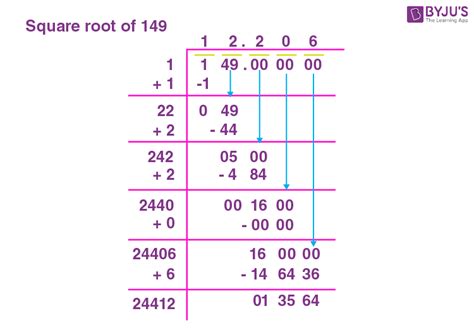
Table of Contents
What is the Square Root of 149? A Deep Dive into Calculation and Approximation
The question, "What is the square root of 149?" seems simple at first glance. However, exploring this seemingly straightforward mathematical problem opens doors to a fascinating world of numerical analysis, approximation techniques, and the historical evolution of mathematical understanding. Let's delve into this topic, examining different methods of calculating the square root of 149 and exploring its significance in various mathematical contexts.
Understanding Square Roots
Before we tackle the square root of 149 specifically, let's establish a foundational understanding of square roots. The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 9 is 3 because 3 multiplied by 3 equals 9. Mathematically, we represent the square root of a number 'x' as √x.
This concept is fundamental to various mathematical operations and applications, appearing in geometry (calculating areas and volumes), physics (solving equations of motion), and countless other fields. Understanding square roots is crucial for navigating more complex mathematical concepts.
Why 149 is Not a Perfect Square
Unlike numbers like 9, 16, or 25, which are perfect squares (meaning their square roots are whole numbers), 149 is not a perfect square. This means its square root is an irrational number – a number that cannot be expressed as a simple fraction and whose decimal representation goes on forever without repeating. This characteristic adds an interesting layer of complexity to the problem of finding its square root.
Methods for Calculating the Square Root of 149
There are several methods for approximating the square root of 149. Let's explore some common techniques:
1. Using a Calculator
The simplest approach is to use a calculator. Most calculators have a dedicated square root function (√). Simply input 149 and press the square root button. The calculator will provide a decimal approximation, typically accurate to several decimal places. This is often the most practical method for everyday purposes, providing a quick and readily available answer. However, it doesn't offer the mathematical understanding behind the calculation.
2. The Babylonian Method (or Heron's Method)
This iterative method is an ancient algorithm for approximating square roots. It refines an initial guess through successive approximations, converging towards the true value. Here's how it works for √149:
- Make an initial guess: Let's start with 12, as 12² = 144, which is close to 149.
- Iterate: The formula for the next guess (xₙ₊₁) is given by: xₙ₊₁ = ½ * (xₙ + 149/xₙ) , where xₙ is the current guess.
- Repeat: Repeat step 2 using the new guess until the desired level of accuracy is achieved.
Let's perform a few iterations:
- Iteration 1: x₁ = ½ * (12 + 149/12) ≈ 12.208
- Iteration 2: x₂ = ½ * (12.208 + 149/12.208) ≈ 12.20655
- Iteration 3: x₃ = ½ * (12.20655 + 149/12.20655) ≈ 12.2065556
As you can see, the value converges rapidly. After just a few iterations, we have a highly accurate approximation of √149. The Babylonian method is a powerful technique, demonstrating how iterative processes can lead to precise results.
3. Newton-Raphson Method
Another powerful iterative method for finding roots is the Newton-Raphson method. This method is particularly useful for finding roots of more complex functions. For finding the square root of 149, we can consider the function f(x) = x² - 149. We're looking for the root of this function (where f(x) = 0). The iterative formula is:
xₙ₊₁ = xₙ - f(xₙ)/f'(xₙ)
where f'(xₙ) is the derivative of f(x) at xₙ. In our case, f'(x) = 2x. Therefore, the iteration formula becomes:
xₙ₊₁ = xₙ - (xₙ² - 149) / (2xₙ) = ½ * (xₙ + 149/xₙ)
Notice that this is identical to the Babylonian method! The Babylonian method is a specific case of the Newton-Raphson method.
4. Linear Approximation
A simpler, though less accurate, approach is linear approximation. We can use the fact that √144 = 12 and √169 = 13. Since 149 lies between 144 and 169, its square root will lie between 12 and 13. We can approximate using a linear interpolation:
√149 ≈ 12 + (149 - 144) * (13 - 12) / (169 - 144) ≈ 12.2
This provides a rough estimate, but it lacks the precision of the iterative methods.
Significance and Applications
Understanding the square root of 149, and the methods used to calculate it, has implications beyond simple numerical computation. The concepts involved are crucial in:
- Numerical Analysis: The iterative methods (Babylonian and Newton-Raphson) are foundational in numerical analysis, used to solve complex equations and approximate solutions where exact solutions are unavailable.
- Computer Science: These algorithms are implemented in computer programs and software to perform square root calculations efficiently.
- Engineering and Physics: Square roots are integral to solving various equations in engineering and physics, such as those related to distance, velocity, and acceleration.
- Geometry: Calculating areas, volumes, and distances often involves square roots. For example, finding the diagonal of a rectangle uses the Pythagorean theorem, which incorporates square roots.
Conclusion
The seemingly simple question of finding the square root of 149 leads to a rich exploration of numerical approximation techniques, algorithm design, and the practical applications of these mathematical concepts. While a calculator provides a quick answer, understanding the underlying methods, such as the Babylonian and Newton-Raphson methods, offers valuable insights into the power and elegance of numerical analysis. The ability to approximate irrational numbers accurately is a fundamental skill in various scientific and engineering disciplines. This deep dive highlights that even seemingly basic mathematical problems can uncover fascinating complexities and have far-reaching implications. Mastering these techniques strengthens your mathematical understanding and equips you with valuable problem-solving skills across various fields.
Latest Posts
Latest Posts
-
Finding The Equation Of A Vertical Line
Apr 06, 2025
-
What Is The Square Root 289
Apr 06, 2025
-
How To Write 45 Minutes As A Decimal
Apr 06, 2025
-
Three To The Power Of Three
Apr 06, 2025
-
How Many Days Is 35 Weeks
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Square Root Of 149 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
