What Is The Value Of 2 3 4 5
News Co
May 08, 2025 · 5 min read
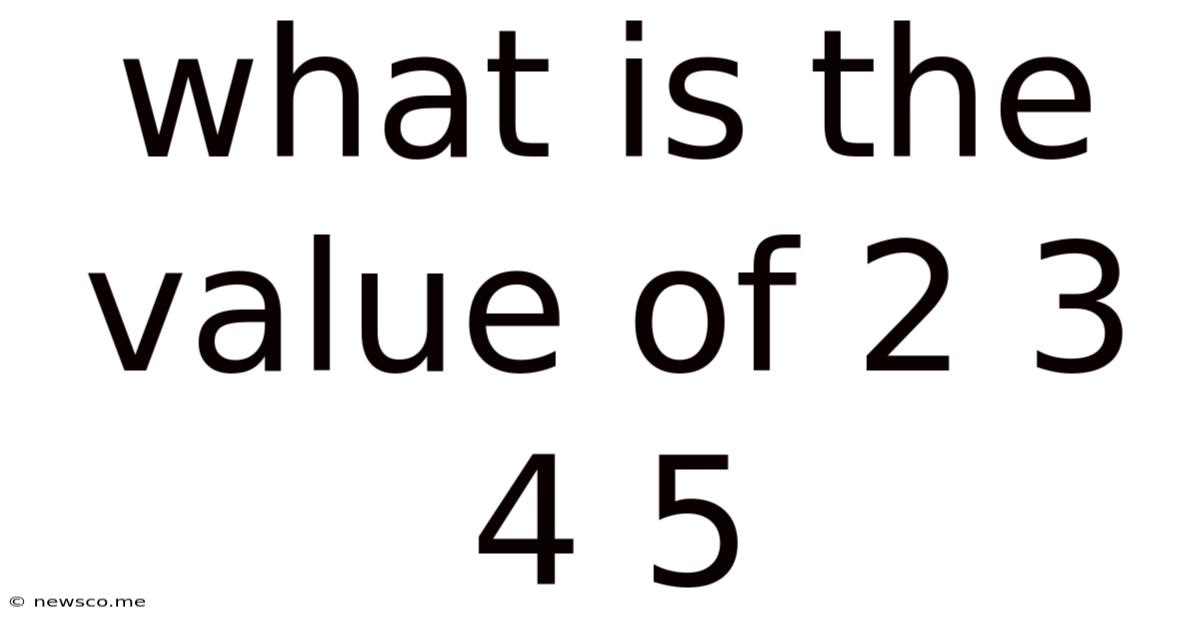
Table of Contents
What is the Value of 2 3 4 5? Exploring Number Sequences, Patterns, and Their Applications
The seemingly simple sequence "2 3 4 5" might appear trivial at first glance. However, depending on the context, this sequence can hold significant mathematical value and represent a variety of concepts. This article delves into the various interpretations and applications of this sequence, exploring its potential meaning within different mathematical fields and real-world scenarios.
Understanding the Context: The Importance of Interpretation
The core value of "2 3 4 5" hinges entirely on its context. Without additional information or a defined pattern, assigning a single "value" is impossible. The sequence could be:
- Part of a larger sequence: It could be the beginning of an arithmetic progression, a geometric progression, or a more complex sequence with a hidden pattern.
- A subset of a set: It could represent a selection from a larger set of numbers, perhaps chosen based on specific criteria.
- Coordinates or data points: In fields like geometry or data analysis, these numbers could represent coordinates or data points with significant meaning.
- A code or cipher: In cryptography, this sequence could be part of a code or cipher needing decryption.
Therefore, analyzing the potential interpretations is crucial to determining its "value."
Mathematical Interpretations of the Sequence 2 3 4 5
Let's explore some potential mathematical interpretations:
1. Arithmetic Progression: The Simplest Interpretation
The most straightforward interpretation of "2 3 4 5" is as the beginning of an arithmetic progression. An arithmetic progression is a sequence where each term is obtained by adding a constant value (the common difference) to the previous term. In this case, the common difference is 1. The sequence continues: 2, 3, 4, 5, 6, 7, 8...
The value in this context isn't a single number but the entire sequence's properties. This includes:
- Common difference: 1
- nth term: The nth term of the sequence can be calculated using the formula: a_n = a_1 + (n-1)d, where a_1 is the first term (2), n is the term number, and d is the common difference (1).
- Sum of the first n terms: The sum of the first n terms can be calculated using the formula: S_n = (n/2)(a_1 + a_n)
2. Geometric Progression: Exploring a Different Pattern
While less obvious, "2 3 4 5" could also be considered the beginning of a non-standard geometric progression. A geometric progression has a constant ratio between consecutive terms. However, finding a constant ratio for this sequence requires a more complex approach, potentially involving non-integer ratios or a more nuanced interpretation of the sequence.
3. Polynomial Representation: A More Advanced Approach
One could model this sequence using a polynomial function. A polynomial of degree n-1 can be fit to n data points. For the sequence "2 3 4 5," a polynomial of degree 3 could be found. This polynomial would represent the sequence, allowing for prediction of subsequent terms and the analysis of the underlying functional relationship. Finding this polynomial involves techniques from numerical analysis and linear algebra.
4. Combinatorics and Permutations: Exploring Arrangements
In combinatorics, the numbers 2, 3, 4, and 5 could represent quantities used in calculations related to permutations, combinations, or other combinatorial problems. For instance:
- Number of permutations: The number of permutations of a set of 5 distinct objects taken 4 at a time is calculated using the formula: P(5,4) = 5!/(5-4)! = 120. This shows that the numbers in the sequence can be building blocks in much larger combinatorial calculations.
- Number of combinations: The number of combinations of choosing 2 objects from a set of 5 is C(5,2) = 10. Again, the sequence elements are part of a larger combinatorial context.
Applications in Real-World Scenarios
Beyond pure mathematics, the sequence "2 3 4 5" could have significance in various real-world applications:
1. Data Analysis and Statistics: Identifying Trends
In data analysis, this sequence might represent a subset of data points. Analyzing the surrounding data could reveal trends, patterns, or anomalies. For example, it could be part of a larger dataset showing an increasing trend in sales, website traffic, or any other quantifiable variable.
2. Computer Science and Programming: Array Indexing or Data Structures
In programming, "2 3 4 5" could represent indices in an array or elements in a data structure. The sequence might be used to access specific elements within a larger data set.
3. Engineering and Physics: Representing Measurements or Physical Quantities
In engineering or physics, these numbers might represent measurements, such as voltage levels, temperatures, or distances. Understanding the sequence's context is crucial in interpreting the measurements and their significance.
4. Cryptography and Security: A Component of a Code
As mentioned earlier, this sequence might be part of a code or cipher. Its value would depend on the specific encryption or decryption method used.
Advanced Concepts and Further Exploration
This exploration only scratches the surface of the potential meanings and values associated with the seemingly simple sequence "2 3 4 5." More advanced interpretations involve:
- Number theory: Exploring the properties of the individual numbers (2, 3, 4, 5) within the context of number theory could reveal interesting connections to prime numbers, divisors, and other number-theoretic concepts.
- Abstract algebra: The sequence could be viewed as elements in a group or a ring, depending on the defined operations.
- Mathematical modeling: More complex models, beyond simple polynomials, could be used to represent the sequence, allowing for more accurate predictions and a deeper understanding of the underlying relationship.
Conclusion: The Value Depends on the Context
In conclusion, the "value" of the sequence "2 3 4 5" is not a single number but depends heavily on its context. Whether interpreted as an arithmetic progression, part of a larger dataset, a code, or an element in a more complex mathematical framework, understanding the sequence's context is key to unlocking its full meaning and potential applications. This exploration highlights the importance of context in mathematics and the diverse ways seemingly simple sequences can have profound implications in various fields. Further research into the specific context where this sequence appears is necessary for a complete and accurate evaluation of its value.
Latest Posts
Latest Posts
-
Draw A Net Of A Triangular Prism
May 08, 2025
-
90 Grados Fahrenheit Es Frio O Calor
May 08, 2025
-
How Many Milliliters Are In 5 Liters
May 08, 2025
-
18 Of What Number Is 90
May 08, 2025
-
Convert 15 Degrees Fahrenheit To Celsius
May 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Value Of 2 3 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.