What Is X 3 Times X 3
News Co
May 08, 2025 · 4 min read
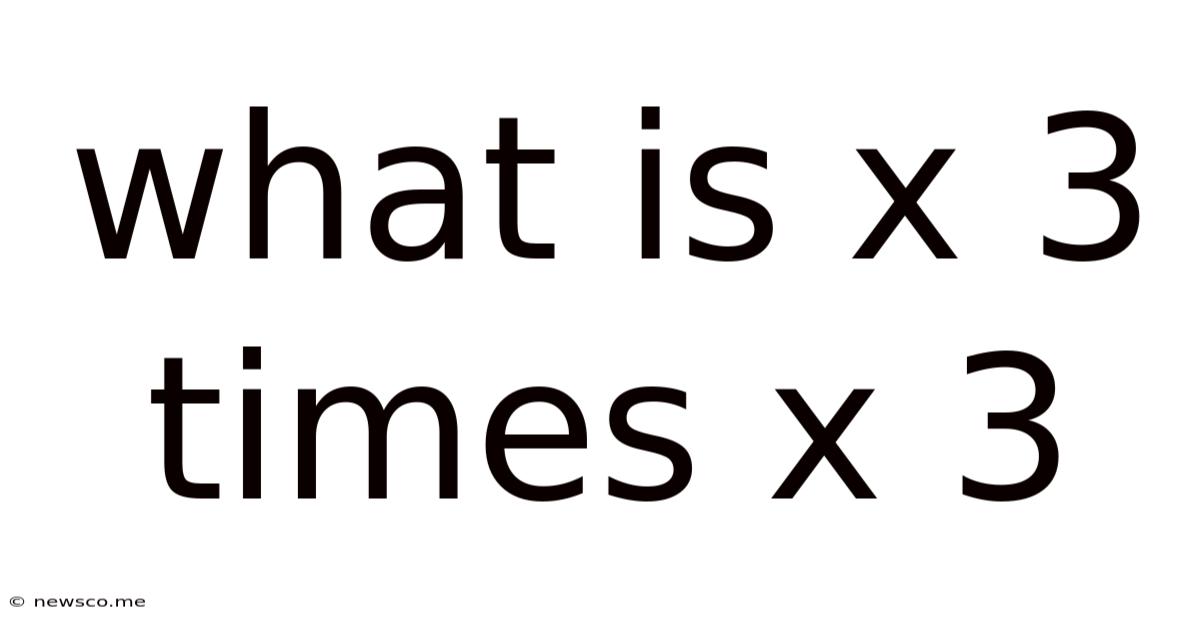
Table of Contents
What is X times 3 times X times 3? A Deep Dive into Mathematical Expressions
The seemingly simple question, "What is X times 3 times X times 3?" opens a door to a fascinating exploration of mathematical notation, algebraic manipulation, and the power of simplification. While the immediate answer might seem straightforward, understanding the underlying principles allows us to tackle far more complex problems with confidence. This article will not only provide the answer but also delve into the conceptual understanding, various representations, and practical applications of this expression.
Understanding the Expression
The expression "X times 3 times X times 3" can be written more concisely using mathematical notation. Multiplication is commutative, meaning the order of the operands doesn't change the result (e.g., 2 x 3 = 3 x 2). Therefore, we can rewrite the expression as:
3 * X * 3 * X
or, more conventionally:
3x * 3x
This is an algebraic expression involving a single variable, 'X', and constants (3). The expression represents the product of two identical terms: 3x and 3x.
Simplifying the Expression
The power of algebra lies in its ability to simplify complex expressions. Our expression can be simplified using the rules of exponents and multiplication.
Recall that:
- a * a = a² (a squared)
Applying this rule to our expression:
(3x) * (3x) = (3 * x * 3 * x) = (3 * 3) * (x * x) = 9x²
Therefore, 3x * 3x = 9x²
This simplified form, 9x², is far more manageable and easier to work with than the original expression. This simplification is crucial in various mathematical applications.
Different Representations of the Expression
The same mathematical concept can be represented in multiple ways. Understanding these variations enhances comprehension and problem-solving skills.
1. Expanded Form:
The initial expression, "X times 3 times X times 3," is an expanded form. It explicitly shows each multiplication operation.
2. Consecutive Multiplication:
We can represent it as consecutive multiplications: 3 * X * 3 * X
3. Parenthetical Grouping:
We can use parentheses to group terms: (3x)(3x) This emphasizes the multiplication of two identical expressions.
4. Exponent Form:
The most simplified form, 9x², uses exponents. This form is highly efficient and commonly used in algebra.
Practical Applications
Understanding how to simplify expressions like "X times 3 times X times 3" is crucial in various fields:
1. Geometry:
Consider calculating the area of a square. If the side length of a square is '3x', the area is given by (3x) * (3x) = 9x². This simple calculation demonstrates the practical application of simplifying algebraic expressions in geometry problems.
2. Physics:
In physics, many equations involve squaring variables. For example, kinetic energy is given by the formula KE = 1/2 * mv², where 'v' represents velocity. Simplifying expressions involving squares is essential for efficient calculation of physical quantities.
3. Computer Programming:
In computer programming, efficient representation of mathematical expressions is crucial for optimizing code performance. Simplifying algebraic expressions directly translates into more efficient code, resulting in faster and more resource-effective programs.
4. Finance:
Compound interest calculations often involve expressions similar to ours. Understanding how to manipulate and simplify such expressions can be invaluable in financial modeling and analysis.
Beyond the Basics: Expanding the Concept
Let's extend our understanding by considering variations and related concepts.
What if the expression was X times 3 times Y times 3?
If the expression were 3 * X * 3 * Y, the simplification would be different:
3 * X * 3 * Y = (3 * 3) * (X * Y) = 9XY
Notice that because X and Y are different variables, they cannot be combined using exponents.
What if the expression involved more terms?
Consider a more complex expression like: X times 3 times X times 3 times X times 3.
This can be rewritten as: (3x)(3x)(3x) = 27x³
This illustrates the extension of the principles of exponents to more complex scenarios.
Mastering Algebraic Manipulation: Tips and Tricks
Mastering algebraic manipulation is a cornerstone of mathematical proficiency. Here are some valuable tips and tricks:
- Understand the order of operations (PEMDAS/BODMAS): This is crucial for correctly evaluating complex expressions. Remember Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
- Practice regularly: The more you practice, the more comfortable you'll become with simplifying expressions. Work through various examples and challenge yourself with increasingly complex problems.
- Break down complex problems: Divide complex expressions into smaller, more manageable parts. This makes the overall simplification process less daunting.
- Utilize online resources: Many online resources, including interactive tutorials and practice problems, can aid your learning.
- Seek help when needed: Don't hesitate to ask for help from teachers, tutors, or peers if you encounter difficulties.
Conclusion
The seemingly simple question, "What is X times 3 times X times 3?" has led us on a journey through fundamental algebraic concepts, simplification techniques, and practical applications. Understanding how to manipulate and simplify algebraic expressions is a crucial skill with far-reaching implications in various fields. By mastering these principles, you enhance your problem-solving capabilities and prepare yourself for more complex mathematical challenges. Remember that consistent practice and a conceptual understanding are key to success in algebra and beyond. The ability to simplify 3x * 3x into 9x² is not just about getting the right answer; it's about understanding the underlying mathematical principles and applying them effectively to diverse problems.
Latest Posts
Latest Posts
-
Lcm Of 7 4 And 2
May 09, 2025
-
How Many Lines Of Symmetry Does Isosceles Triangle Have
May 09, 2025
-
What Is The Graph Of 3x 5y 15
May 09, 2025
-
How To Find Domain Of Composite Functions
May 09, 2025
-
Can Sample Variance Be Equal To Population Variance
May 09, 2025
Related Post
Thank you for visiting our website which covers about What Is X 3 Times X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.