What's The Greatest Common Factor Of 8 And 12
News Co
Apr 05, 2025 · 5 min read
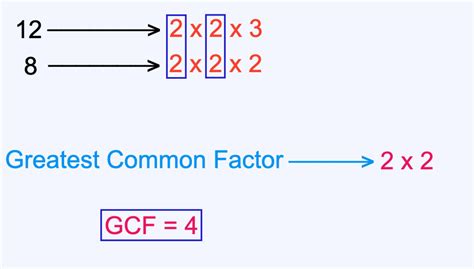
Table of Contents
What's the Greatest Common Factor of 8 and 12? A Deep Dive into Number Theory
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, suitable only for elementary school students. However, understanding the concept of GCF and the various methods to calculate it delves into fundamental principles of number theory with surprisingly broad applications in mathematics, computer science, and even music theory. This article will explore the GCF of 8 and 12 in detail, examining various methods for its calculation and highlighting its significance in a wider mathematical context.
Understanding the Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes evenly into both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 without leaving a remainder.
Why is the GCF Important?
The GCF plays a crucial role in various mathematical operations and applications:
-
Simplifying Fractions: The GCF is essential for reducing fractions to their simplest form. For example, the fraction 12/18 can be simplified to 2/3 by dividing both the numerator and denominator by their GCF, which is 6.
-
Solving Equations: GCF is used in solving Diophantine equations, which are equations where only integer solutions are sought.
-
Algebraic Manipulation: Finding the GCF is crucial when factoring algebraic expressions. This simplification makes solving equations and other algebraic manipulations much easier.
-
Geometry: The GCF is often used in geometric problems involving area and perimeter calculations.
Methods for Finding the GCF of 8 and 12
Let's now focus on finding the GCF of 8 and 12 using several common methods.
1. Listing Factors Method
This is a straightforward method, particularly useful for smaller numbers. We list all the factors of each number and then identify the largest factor common to both.
Factors of 8: 1, 2, 4, 8 Factors of 12: 1, 2, 3, 4, 6, 12
Comparing the lists, we see that the common factors are 1, 2, and 4. The greatest of these common factors is 4. Therefore, the GCF of 8 and 12 is 4.
2. Prime Factorization Method
This method utilizes the prime factorization of each number. The prime factorization is the representation of a number as a product of its prime factors (numbers divisible only by 1 and themselves).
- Prime factorization of 8: 2 x 2 x 2 = 2³
- Prime factorization of 12: 2 x 2 x 3 = 2² x 3
To find the GCF, we identify the common prime factors and multiply them together, using the lowest power of each common factor. In this case, the common prime factor is 2, and the lowest power is 2². Therefore, the GCF is 2² = 4.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal.
- Start with the two numbers: 8 and 12.
- Divide the larger number (12) by the smaller number (8): 12 = 8 x 1 + 4
- Replace the larger number (12) with the remainder (4): Now we have 8 and 4.
- Repeat the process: 8 = 4 x 2 + 0
- The process stops when the remainder is 0. The GCF is the last non-zero remainder, which is 4.
Applications of GCF: Real-World Examples
The GCF isn't just a theoretical concept; it has practical applications in various fields:
1. Geometry
Imagine you're tiling a rectangular floor with square tiles. The dimensions of the floor are 8 feet by 12 feet. To find the largest square tile that can be used without cutting any tiles, you need to find the GCF of 8 and 12. As we've determined, the GCF is 4. Therefore, the largest square tile you can use is 4 feet by 4 feet.
2. Music Theory
In music, the GCF plays a role in determining the simplest form of a musical interval. For example, consider two notes with frequencies of 8 Hz and 12 Hz. The GCF of 8 and 12 is 4. This means that the ratio of their frequencies can be simplified to 2:3, which represents a perfect fifth interval.
3. Computer Science
The Euclidean algorithm, used to find the GCF, is fundamental in computer science, particularly in cryptography. It's used in modular arithmetic calculations, which are critical in the implementation of various encryption algorithms.
Extending the Concept: Least Common Multiple (LCM)
Closely related to the GCF is the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. For 8 and 12, the LCM is 24. The GCF and LCM are connected through the following relationship:
GCF(a, b) x LCM(a, b) = a x b
In our case, GCF(8, 12) x LCM(8, 12) = 4 x 24 = 96, and 8 x 12 = 96, confirming the relationship.
Conclusion: The Power of Simple Arithmetic
While finding the greatest common factor of 8 and 12 might seem trivial at first glance, it exemplifies a fundamental concept in number theory with far-reaching applications. Understanding the GCF, the different methods for calculating it, and its connections to other mathematical concepts like LCM is crucial for a deeper appreciation of mathematics and its relevance in various disciplines. From simplifying fractions to solving complex equations and even understanding musical intervals, the GCF’s influence is surprisingly pervasive. This seemingly simple arithmetic operation holds a significant and powerful position within the broader mathematical landscape. Mastering the concept of GCF opens doors to a deeper understanding of number theory and its real-world implications.
Latest Posts
Latest Posts
-
Whats The Difference Between A Meter And A Yard
Apr 06, 2025
-
How To Make A Perfect Square
Apr 06, 2025
-
Area Of Irregular Figures Worksheet Answers
Apr 06, 2025
-
What Is The Reflexive Property Of Congruence
Apr 06, 2025
-
How Many Oz Of Water Make A Gallon
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What's The Greatest Common Factor Of 8 And 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
