Worksheet Triangle Sum And Exterior Angle Theorem
News Co
Apr 05, 2025 · 6 min read
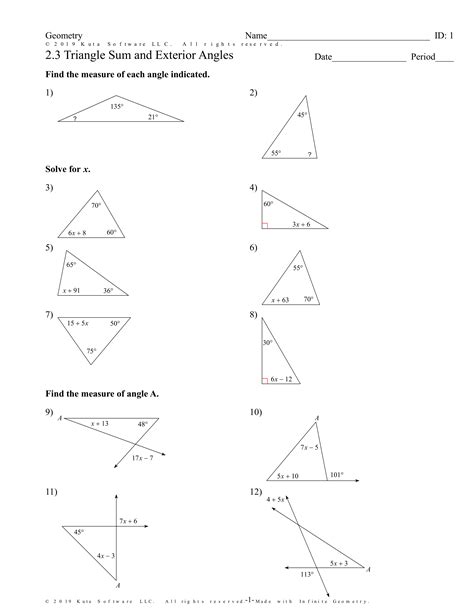
Table of Contents
Worksheet: Triangle Sum and Exterior Angle Theorem
Understanding triangles is fundamental to geometry. This worksheet delves into two crucial theorems concerning triangles: the Triangle Sum Theorem and the Exterior Angle Theorem. Mastering these theorems will significantly improve your geometrical problem-solving skills. We'll explore the theorems, delve into example problems, and provide practice exercises to solidify your understanding.
The Triangle Sum Theorem: The Foundation of Triangles
The Triangle Sum Theorem is a cornerstone of geometry. It states that the sum of the interior angles of any triangle always equals 180 degrees. This applies to all triangles, regardless of their shape or size – acute, obtuse, right, equilateral, isosceles; the sum of their interior angles remains a constant 180°.
Understanding the Theorem
This theorem is based on the fundamental principles of parallel lines and transversals. Consider a triangle ABC. If you extend one side (say, BC) to form a line, you create an exterior angle. Drawing a line parallel to BC through A intersects the extended line and creates corresponding angles that are equal to the interior angles of the triangle. The sum of these angles, forming a straight line (180°), proves the theorem.
Proof of the Triangle Sum Theorem
Let's formalize the proof:
- Draw a triangle ABC.
- Draw a line parallel to BC through point A.
- Observe the angles formed by the parallel line and the transversal lines AB and AC.
- Apply the corresponding angles postulate: Angle 1 is equal to angle B, and angle 2 is equal to angle C.
- The sum of angles on a straight line is 180°: Angle 1 + angle A + angle 2 = 180°.
- Substitution: Since angle 1 = angle B and angle 2 = angle C, substitute these values into the equation: angle B + angle A + angle C = 180°.
Therefore, the sum of the interior angles of triangle ABC is 180°. This proof holds true for all types of triangles.
Applications of the Triangle Sum Theorem
The Triangle Sum Theorem allows us to solve for unknown angles within a triangle. If we know two angles, we can easily find the third. This has numerous applications in geometry problems, including:
- Finding missing angles: Given two angles of a triangle, you can find the third using the equation: Missing Angle = 180° - (Angle 1 + Angle 2).
- Classifying triangles: The theorem helps classify triangles based on their angles (acute, obtuse, right). If all angles are less than 90°, it's an acute triangle. If one angle is greater than 90°, it's an obtuse triangle. If one angle is exactly 90°, it's a right triangle.
- Solving complex geometric problems: The theorem can be combined with other geometrical principles to solve more intricate problems involving triangles.
The Exterior Angle Theorem: Extending the Boundaries
The Exterior Angle Theorem builds upon the Triangle Sum Theorem. It states that the measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.
Understanding the Theorem
An exterior angle is formed when one side of a triangle is extended. The exterior angle lies outside the triangle and is supplementary (adds up to 180°) to the adjacent interior angle. The theorem states that the exterior angle is equal to the sum of the two remote (non-adjacent) interior angles.
Proof of the Exterior Angle Theorem
Let's prove the Exterior Angle Theorem:
- Consider triangle ABC.
- Extend side BC to form an exterior angle at C, labeled as angle DCE.
- The sum of interior angles in a triangle is 180° (Triangle Sum Theorem): angle A + angle B + angle ACB = 180°.
- Angles on a straight line add up to 180°: angle ACB + angle DCE = 180°.
- From steps 3 and 4: angle A + angle B + angle ACB = angle ACB + angle DCE.
- Subtracting angle ACB from both sides: angle A + angle B = angle DCE.
This proves that the exterior angle (angle DCE) is equal to the sum of the two remote interior angles (angle A and angle B).
Applications of the Exterior Angle Theorem
The Exterior Angle Theorem provides a shortcut for finding angles in triangles, often simplifying problem-solving:
- Finding exterior angles: Given two remote interior angles, you can easily find the measure of the exterior angle.
- Finding interior angles: If you know an exterior angle and one remote interior angle, you can find the other remote interior angle.
- Simplifying problem-solving: The theorem can significantly streamline geometric proofs and problems, reducing the number of steps needed.
Practice Problems: Putting it all Together
Here are some practice problems to test your understanding of the Triangle Sum and Exterior Angle Theorems:
Problem 1:
In triangle XYZ, angle X = 50° and angle Y = 70°. Find the measure of angle Z.
Solution: Using the Triangle Sum Theorem, angle Z = 180° - (50° + 70°) = 60°.
Problem 2:
In triangle PQR, angle P = 45° and angle Q = 65°. Find the measure of the exterior angle at R.
Solution: The exterior angle at R is equal to the sum of angles P and Q. Therefore, the exterior angle = 45° + 65° = 110°.
Problem 3:
In triangle ABC, the exterior angle at A is 120°. Angle B is 50°. Find the measure of angle C.
Solution: The exterior angle at A equals the sum of angles B and C. Therefore, 120° = 50° + angle C. Solving for angle C, we get angle C = 70°.
Problem 4:
A triangle has angles measuring x, 2x, and 3x. Find the value of x and the measure of each angle.
Solution: Using the Triangle Sum Theorem: x + 2x + 3x = 180°. This simplifies to 6x = 180°, so x = 30°. Therefore, the angles are 30°, 60°, and 90°. This is a special right-angled triangle – a 30-60-90 triangle.
Problem 5 (Challenging):
Two angles of a triangle are equal. The third angle is twice the measure of each of the equal angles. Find the measure of all three angles.
Solution: Let the equal angles be x. The third angle is 2x. Therefore, x + x + 2x = 180°. This simplifies to 4x = 180°, so x = 45°. The angles are 45°, 45°, and 90°. This is another special right-angled triangle – an isosceles right-angled triangle.
Advanced Applications and Extensions
The Triangle Sum and Exterior Angle Theorems form the basis for many advanced geometrical concepts. They are frequently used in:
- Trigonometry: These theorems are crucial for understanding trigonometric functions and solving triangles using sine, cosine, and tangent rules.
- Coordinate Geometry: Finding the angles and lengths of triangles on a coordinate plane often relies on these theorems.
- Three-dimensional Geometry: Similar principles apply to finding angles and solving problems in three dimensions.
- Proofs: These theorems are building blocks in many geometric proofs.
Conclusion
Mastering the Triangle Sum and Exterior Angle Theorems is essential for success in geometry. By understanding these theorems and their applications, you will be well-equipped to solve a wide range of geometric problems. Remember to practice regularly, and you'll soon find that applying these theorems becomes second nature. These theorems are not just abstract concepts; they are practical tools for navigating the world of shapes and angles. They underpin more complex geometrical concepts, making their mastery a crucial step in your mathematical journey. Continue to explore these concepts and expand your geometrical knowledge.
Latest Posts
Latest Posts
-
Sum Of Interior Angles Of Hexagon
Apr 06, 2025
-
What Is The Square Root Of 252
Apr 06, 2025
-
Ordering Fractions From Least To Greatest Worksheet
Apr 06, 2025
-
What Is The Basic Metric Unit Of Length
Apr 06, 2025
-
3 T 3 5 2t 1
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Worksheet Triangle Sum And Exterior Angle Theorem . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
