X 3 X 2 X 2
News Co
May 08, 2025 · 5 min read
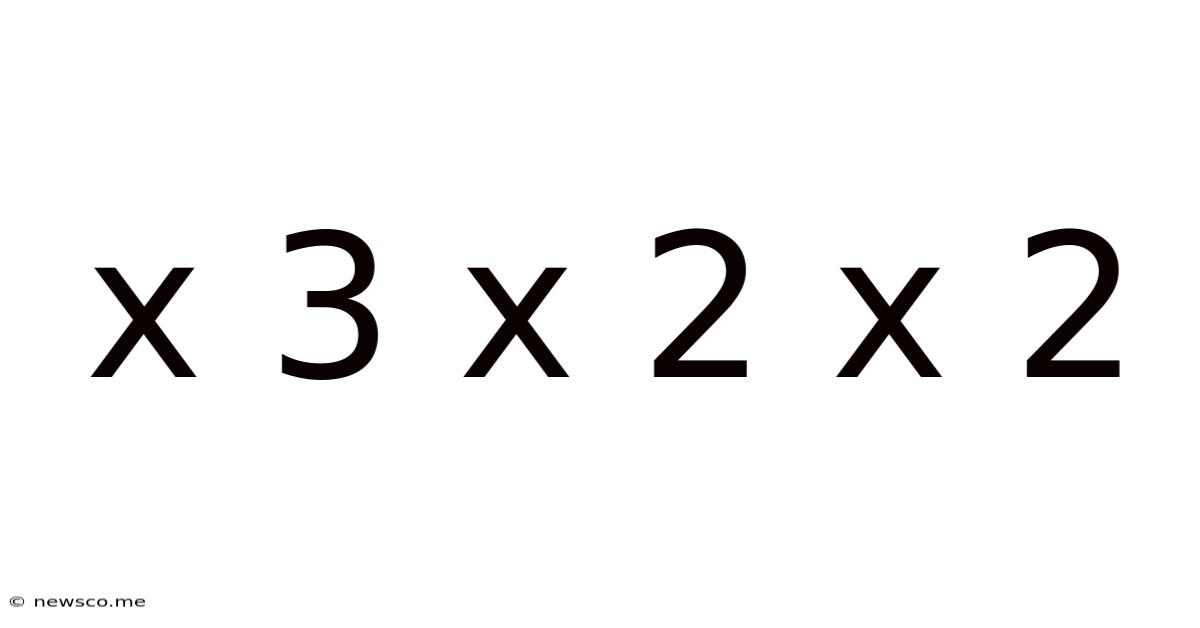
Table of Contents
Decoding the Mystery: A Deep Dive into x³ x² x²
The seemingly simple expression "x³ x² x²" presents a fascinating opportunity to explore several key mathematical concepts. While the initial appearance suggests a straightforward calculation, a deeper analysis reveals intricacies involving exponents, algebraic simplification, and even potential applications in various fields. This comprehensive guide will dissect this expression, unveiling its underlying mechanisms and showcasing its relevance beyond basic arithmetic.
Understanding the Fundamentals: Exponents and Multiplication
Before diving into the intricacies of the expression, it's crucial to establish a strong foundation in exponents and their properties. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. In our expression, 'x' represents the base, while the superscript numbers (3, 2, and 2) denote the exponents.
- x³ (x cubed): This means x multiplied by itself three times: x * x * x.
- x² (x squared): This means x multiplied by itself twice: x * x.
Therefore, our expression "x³ x² x²" can be expanded as: (x * x * x) * (x * x) * (x * x).
The Power of Rules: Simplifying Exponential Expressions
The key to simplifying this expression lies in understanding the rules of exponents. Specifically, when multiplying terms with the same base, we add their exponents. This rule significantly streamlines our calculation:
x³ x² x² = x⁽³⁺²⁺²⁾ = x⁷
Thus, the simplified form of "x³ x² x²" is x⁷ (x to the power of 7). This means x multiplied by itself seven times. This simplification demonstrates the elegance and efficiency of algebraic manipulation.
Beyond the Basics: Exploring Applications and Extensions
While the simplification is straightforward, the underlying principles have far-reaching implications across various mathematical and scientific domains. Let's explore some examples:
1. Polynomial Arithmetic and Algebra
This simple expression forms a building block for more complex polynomial expressions. Polynomials are algebraic expressions consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents. Understanding the simplification of "x³ x² x²" is fundamental to manipulating and solving polynomial equations, which are crucial in numerous fields, including:
- Physics: Describing the motion of projectiles, analyzing oscillations, and modeling complex systems.
- Engineering: Designing structures, analyzing circuits, and optimizing processes.
- Economics: Building models for growth, predicting market trends, and analyzing financial instruments.
- Computer Science: Developing algorithms, analyzing data structures, and creating mathematical models for simulations.
2. Calculus and Differential Equations
The concept of exponents is central to calculus, the study of continuous change. Derivatives and integrals, the fundamental building blocks of calculus, heavily rely on the rules of exponents. Understanding how to manipulate expressions like "x³ x² x²" is essential for:
- Finding rates of change: Calculating velocity, acceleration, and other dynamic quantities.
- Determining areas and volumes: Solving integration problems crucial in various applications.
- Solving differential equations: Modeling dynamic systems and processes across numerous fields (physics, engineering, biology).
3. Geometric Interpretations and Volume Calculations
While the expression itself doesn't directly represent a geometric shape, the underlying concept of exponents often arises in geometric calculations. Consider, for example, the volume of a cube. If the side length of the cube is 'x', then its volume is x³. If we were to consider manipulating cubes, perhaps combining smaller cubes to form a larger structure, the principles of multiplying exponential expressions would be highly relevant.
4. Financial Modeling and Compound Interest
The concept of exponents also plays a vital role in financial calculations, particularly in understanding compound interest. Compound interest involves earning interest not only on the principal amount but also on accumulated interest. The formula for compound interest includes exponents, and the ability to simplify exponential expressions is beneficial for analyzing investment growth.
Imagine an investment that grows exponentially. Let's say the initial investment is 'x' and it doubles every year. After three years, the investment would be 2³x = 8x. This example showcases the practical relevance of exponents in financial modeling and investment planning.
Expanding the Horizons: Exploring Variations and Extensions
While we have focused on the specific expression "x³ x² x²," the principles explored here can be readily applied to a wider range of exponential expressions. Let's consider some variations:
- Different Bases: The same rules apply if we replace 'x' with any other variable or number. For example, (2³) (2²) (2²) would simplify to 2⁷ = 128.
- Negative Exponents: The rules for exponents also extend to negative exponents. Recall that x⁻ⁿ = 1/xⁿ.
- Fractional Exponents: Fractional exponents represent roots. For example, x^(1/2) is the square root of x. Combining fractional and integer exponents requires a deeper understanding of exponent rules but follows consistent principles.
- More Complex Expressions: The same principles can be applied to expressions with multiple terms and variables. For example, simplifying (2x³y²) (3x²y) requires applying the distributive property and the rules of exponents.
Conclusion: The Power of Understanding
The seemingly simple expression "x³ x² x²" serves as a gateway to understanding fundamental concepts in algebra, calculus, and various scientific fields. Its simplification to x⁷ reveals the power and elegance of mathematical manipulation. The underlying principles of exponents, when grasped firmly, unlock the ability to solve complex problems, analyze dynamic systems, and make accurate predictions across diverse disciplines. This exploration extends beyond rote memorization of formulas; it encourages a deeper understanding of the interconnectedness of mathematical concepts and their practical applications in the real world. By understanding and applying these principles, you build a strong foundation for tackling more advanced mathematical challenges and applying your skills to a vast array of real-world scenarios.
Latest Posts
Latest Posts
-
5000 Meter Is How Many Miles
May 08, 2025
-
79 8 As A Mixed Number
May 08, 2025
-
How Many Weeks Are In Five Months
May 08, 2025
-
2x 3 X 2 X 3
May 08, 2025
-
Find A Unit Vector That Is Orthogonal To Both And
May 08, 2025
Related Post
Thank you for visiting our website which covers about X 3 X 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.