Y 1 X 1 Domain And Range
News Co
May 08, 2025 · 5 min read
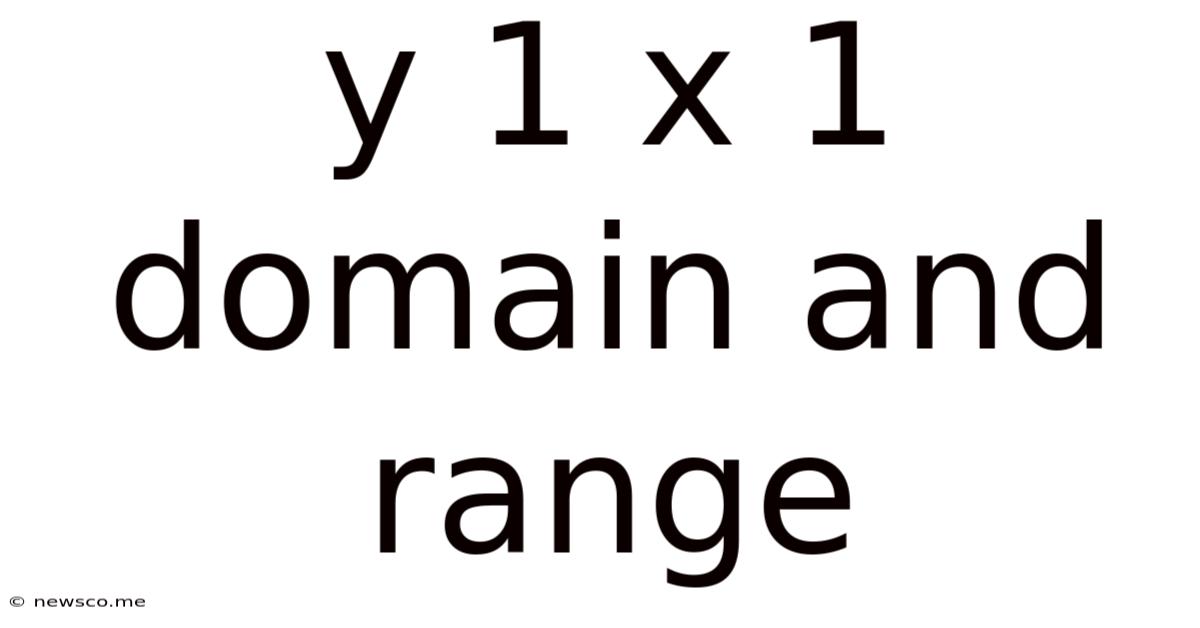
Table of Contents
Understanding the Domain and Range of y = 1/x: A Comprehensive Guide
The function y = 1/x, also known as the reciprocal function or inverse function, is a fundamental concept in algebra and calculus. Understanding its domain and range is crucial for grasping its behavior and applying it in various mathematical contexts. This comprehensive guide will delve into the intricacies of the function y = 1/x, exploring its domain, range, and related properties. We will also examine its graph and discuss how these concepts apply to real-world applications.
Defining Domain and Range
Before diving into the specifics of y = 1/x, let's solidify our understanding of domain and range.
Domain
The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. In simpler terms, it's the set of all x-values that you can plug into the function and get a valid output (y-value).
Range
The range of a function is the set of all possible output values (y-values) that the function can produce. It's the set of all y-values that the function can take on.
Determining the Domain and Range of y = 1/x
Now, let's analyze the function y = 1/x. The key to determining its domain and range lies in identifying any restrictions on the input (x) that would lead to an undefined output (y).
The Restriction: Division by Zero
The most significant restriction in y = 1/x is the potential for division by zero. Division by zero is undefined in mathematics. Therefore, we must exclude any x-value that would result in the denominator becoming zero.
In our function, y = 1/x, the denominator is 'x'. The only value of x that makes the denominator zero is x = 0.
Therefore, the domain of y = 1/x is all real numbers except 0. This can be written in interval notation as (-∞, 0) U (0, ∞). The 'U' symbol represents the union of the two intervals.
Determining the Range
To find the range, we consider the possible output values (y-values) that the function can produce. As x approaches positive infinity, y approaches 0 from the positive side (0+). As x approaches negative infinity, y approaches 0 from the negative side (0-). As x approaches 0 from the positive side, y approaches positive infinity. As x approaches 0 from the negative side, y approaches negative infinity.
This behavior demonstrates that y can take on any value except 0. No matter how large or small we make x, we can never obtain a y-value of exactly 0.
Therefore, the range of y = 1/x is all real numbers except 0. This is also represented in interval notation as (-∞, 0) U (0, ∞).
Graphical Representation of y = 1/x
The graph of y = 1/x visually confirms our findings about its domain and range. The graph consists of two separate branches:
-
Branch 1: Located in the first quadrant (where both x and y are positive), this branch approaches the x-axis (y = 0) and the y-axis (x = 0) asymptotically. This means it gets infinitely close to these axes but never touches them.
-
Branch 2: Located in the third quadrant (where both x and y are negative), this branch mirrors the behavior of Branch 1, approaching the axes asymptotically.
The graph clearly shows that there are no points on the graph where x = 0 or y = 0, reinforcing our determination of the domain and range.
Asymptotes: Understanding the Behavior Near the Restrictions
The graph of y = 1/x exhibits asymptotes. An asymptote is a line that a curve approaches arbitrarily closely, but never touches. In this case, we have two asymptotes:
-
Vertical Asymptote: The vertical line x = 0 (the y-axis) acts as a vertical asymptote. The function's value approaches infinity as x approaches 0 from the right and negative infinity as x approaches 0 from the left.
-
Horizontal Asymptote: The horizontal line y = 0 (the x-axis) acts as a horizontal asymptote. The function's value approaches 0 as x approaches positive or negative infinity.
Transformations of y = 1/x
Understanding the domain and range of y = 1/x is crucial when considering transformations of this function. Transformations such as shifting, stretching, and reflecting will alter the graph, but the fundamental concepts of domain and range will guide you in understanding the modified function.
For example:
-
y = 1/(x + 2): This shifts the graph two units to the left. The vertical asymptote moves to x = -2, and the domain becomes (-∞, -2) U (-2, ∞). The range remains (-∞, 0) U (0, ∞).
-
y = 1/x + 3: This shifts the graph three units upward. The horizontal asymptote moves to y = 3, and the range becomes (-∞, 3) U (3, ∞). The domain remains (-∞, 0) U (0, ∞).
-
y = 2/x: This stretches the graph vertically by a factor of 2. The domain and range remain the same.
-
y = -1/x: This reflects the graph across the x-axis. The domain and range remain the same.
Real-world Applications
The reciprocal function, y = 1/x, has numerous applications in various fields:
-
Physics: Inverse square laws, such as Newton's Law of Universal Gravitation and Coulomb's Law, are described using reciprocal functions. These laws describe how the force between two objects decreases as the distance between them increases.
-
Economics: The relationship between supply and demand can sometimes be modeled using reciprocal functions. As the price of a good increases, the quantity demanded may decrease inversely.
-
Computer Science: In algorithms and data structures, reciprocal functions can represent certain time complexities or relationships between data elements.
-
Engineering: Reciprocal functions find use in analyzing electrical circuits and mechanical systems, where impedance and resistance relationships play a role.
Conclusion
The function y = 1/x, while seemingly simple, showcases important concepts in mathematics, particularly concerning domain, range, and asymptotes. Understanding its behavior and properties is essential for solving various mathematical problems and applying the function in real-world scenarios. By grasping the core concepts explored here, you'll gain a solid foundation for tackling more complex mathematical challenges involving reciprocal functions and their transformations. Remember to always consider the restrictions on the input values to accurately determine the domain and the resulting output values to understand the range of any given function.
Latest Posts
Latest Posts
-
What Is 30 Percent Off 20 Dollars
May 08, 2025
-
Sum Of The Solutions Of A Quadratic Equation
May 08, 2025
-
50 Is 20 Percent Of What Number
May 08, 2025
-
Finding Vertex By Completing The Square
May 08, 2025
-
What Is The Measurement Of The Angle Shown Below
May 08, 2025
Related Post
Thank you for visiting our website which covers about Y 1 X 1 Domain And Range . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.