15 Percent Of What Number Is 60
News Co
May 08, 2025 · 5 min read
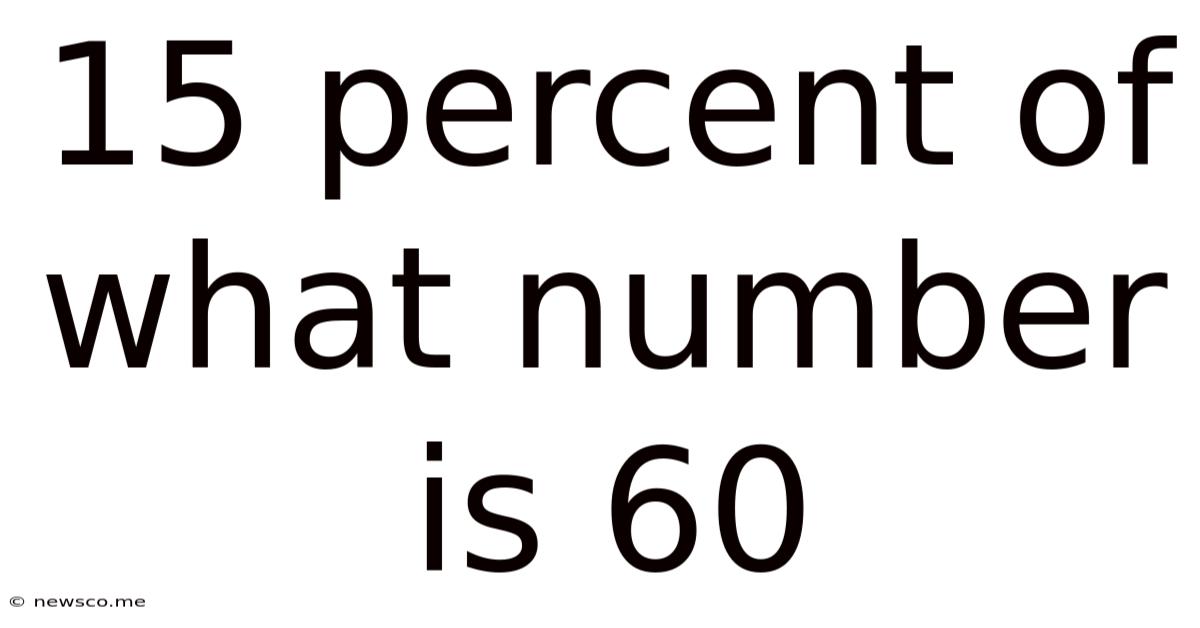
Table of Contents
15 Percent of What Number is 60? A Comprehensive Guide to Percentage Calculations
Finding out "15 percent of what number is 60" isn't just a simple math problem; it's a fundamental concept with wide-ranging applications in various fields, from finance and budgeting to sales and statistics. Understanding how to solve this type of problem is crucial for anyone looking to improve their numeracy skills and confidently tackle real-world percentage calculations. This comprehensive guide will walk you through different methods to solve this specific problem and equip you with the knowledge to tackle similar percentage questions with ease.
Understanding Percentages
Before diving into the solution, let's refresh our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. For example, 15% means 15 out of 100, which can be written as the fraction 15/100 or the decimal 0.15. Percentages are a convenient way to represent proportions and changes, allowing for easy comparison and understanding of relative values.
Method 1: Using the Percentage Formula
The most straightforward method to solve "15 percent of what number is 60" is by using the basic percentage formula:
Percentage = (Part / Whole) x 100
In our problem:
- Percentage: 15% (or 0.15 as a decimal)
- Part: 60
- Whole: This is what we need to find (let's represent it with 'x')
Substituting these values into the formula, we get:
15 = (60 / x) x 100
Now, let's solve for 'x':
- Divide both sides by 100: 0.15 = 60 / x
- Multiply both sides by x: 0.15x = 60
- Divide both sides by 0.15: x = 60 / 0.15
- Calculate the result: x = 400
Therefore, 15% of 400 is 60.
Method 2: Setting up a Proportion
Another effective approach involves setting up a proportion. A proportion is a statement that two ratios are equal. We can set up a proportion based on the given information:
15/100 = 60/x
This proportion reads: "15 is to 100 as 60 is to x." To solve for x, we can cross-multiply:
15x = 6000
Now, divide both sides by 15:
x = 400
Again, we arrive at the same answer: 15% of 400 is 60.
Method 3: Using Decimal Equivalents
Percentages can be easily converted into decimals. 15% is equivalent to 0.15. We can rewrite the problem as:
0.15 * x = 60
To solve for x, we simply divide both sides by 0.15:
x = 60 / 0.15 = 400
This method provides a concise and efficient way to solve the problem, particularly when dealing with simpler percentage calculations.
Practical Applications of Percentage Calculations
The ability to solve percentage problems like "15 percent of what number is 60" has numerous real-world applications:
1. Finance and Budgeting:
- Calculating interest: Understanding percentages is vital for calculating simple and compound interest on loans, investments, and savings accounts.
- Analyzing financial statements: Financial reports often present data as percentages, making it essential to understand how to interpret and analyze this information.
- Budgeting and expense tracking: Percentages help track spending against income and identify areas for potential savings.
2. Sales and Marketing:
- Calculating discounts and markups: Determining the original price after a percentage discount or the selling price after a markup requires using percentage calculations.
- Analyzing sales data: Tracking sales growth or decline as percentages provides valuable insights for business decisions.
- Determining profit margins: Calculating profit margins as percentages helps assess the profitability of products and services.
3. Statistics and Data Analysis:
- Representing proportions and changes: Percentages provide a concise way to represent proportions within data sets and demonstrate changes over time.
- Interpreting statistical data: Understanding percentages is crucial for interpreting statistical analyses and research findings.
- Calculating probabilities: Probability is often expressed as percentages, making it essential to understand percentage calculations in probability problems.
4. Everyday Life:
- Calculating tips and taxes: Determining the amount of tip to leave at a restaurant or calculating sales tax on purchases involves percentage calculations.
- Understanding surveys and polls: Interpreting survey results and poll data often involves understanding percentage representation of opinions and preferences.
- Comparing prices and values: Percentages help compare prices of different products or the value of different investments.
Advanced Percentage Problems and Techniques
While the problem "15 percent of what number is 60" is relatively straightforward, understanding the underlying principles allows you to tackle more complex percentage calculations. These might involve:
- Multiple percentage changes: Calculating the final value after multiple percentage increases or decreases.
- Percentage increase or decrease: Finding the percentage change between two values.
- Compounding percentages: Understanding how percentages compound over time, especially important in financial calculations.
Mastering the fundamental techniques discussed above—using the percentage formula, setting up proportions, and employing decimal equivalents—builds a strong foundation for tackling these advanced problems.
Tips for Mastering Percentage Calculations
- Practice regularly: Consistent practice is key to improving your skills and building confidence in handling percentage problems.
- Use visual aids: Diagrams, charts, and other visual representations can help visualize the relationships between percentages and numbers.
- Break down complex problems: Divide complex problems into smaller, more manageable steps.
- Check your work: Always double-check your calculations to avoid errors.
- Utilize online resources: Numerous online calculators and tutorials can help you practice and reinforce your understanding of percentage calculations.
Conclusion
Solving "15 percent of what number is 60" is a stepping stone to mastering a fundamental mathematical concept with broad practical applications. By understanding the different methods—using the percentage formula, setting up proportions, and working with decimal equivalents—you'll be equipped to confidently handle various percentage calculations in your personal and professional life. Regular practice and a clear understanding of the underlying principles will solidify your skills and enable you to tackle more advanced percentage problems with ease and accuracy. Remember, consistent practice is the key to mastering this crucial skill.
Latest Posts
Latest Posts
-
0 15 Rounded To The Nearest Tenth
May 09, 2025
-
How To Know If A Function Is Rational
May 09, 2025
-
What Is The Measure Of Angle M
May 09, 2025
-
Which Square Root Is Between 4 And 5
May 09, 2025
-
20 Percent Of What Number Is 40
May 09, 2025
Related Post
Thank you for visiting our website which covers about 15 Percent Of What Number Is 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.