21 16 As A Mixed Number
News Co
May 07, 2025 · 5 min read
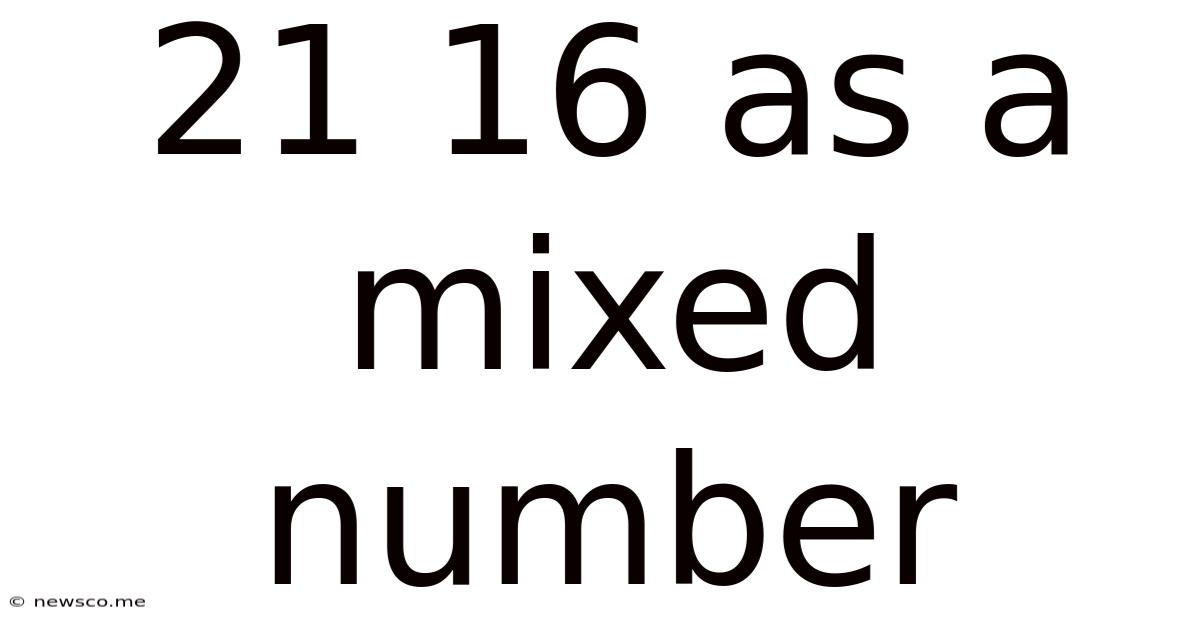
Table of Contents
21/16 as a Mixed Number: A Comprehensive Guide
Converting improper fractions, like 21/16, into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert 21/16 into a mixed number but also delve into the underlying concepts, provide practical examples, and explore related topics to solidify your understanding. We'll even tackle some common misconceptions and offer tips for mastering fraction manipulation.
Understanding Improper Fractions and Mixed Numbers
Before diving into the conversion, let's define our terms:
-
Improper Fraction: An improper fraction is a fraction where the numerator (top number) is greater than or equal to the denominator (bottom number). 21/16 is an example of an improper fraction because 21 (numerator) is greater than 16 (denominator).
-
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator is less than the denominator.
The conversion process essentially involves separating the whole number part from the fractional part of an improper fraction.
Converting 21/16 to a Mixed Number: The Step-by-Step Process
The conversion of 21/16 to a mixed number involves a simple division process:
-
Divide the numerator by the denominator: Divide 21 by 16.
21 ÷ 16 = 1 with a remainder of 5
-
The quotient becomes the whole number: The quotient (the result of the division) is 1. This will be the whole number part of our mixed number.
-
The remainder becomes the new numerator: The remainder is 5. This becomes the numerator of the fractional part of our mixed number.
-
The denominator remains the same: The denominator stays as 16.
-
Combine the whole number and the fraction: Therefore, 21/16 as a mixed number is 1 5/16.
Visualizing the Conversion
Imagine you have 21 pizzas, and each pizza is cut into 16 slices. You can give each person a whole pizza (16 slices) and still have 5 slices left over. This "one whole pizza and 5/16 of a pizza" is represented by the mixed number 1 5/16.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in various real-life scenarios:
-
Cooking and Baking: Recipes often call for mixed numbers of cups, teaspoons, or tablespoons of ingredients. For instance, a recipe might require 2 1/2 cups of flour.
-
Measurements: Measuring lengths, weights, or volumes frequently involves mixed numbers. A carpenter might measure a board as 3 3/4 feet long.
-
Time: Time is often expressed using mixed numbers. For example, 1 hour and 30 minutes can be written as 1 1/2 hours.
Converting Mixed Numbers back to Improper Fractions
It's equally important to understand how to convert a mixed number back into an improper fraction. This is the reverse process of what we just did. Let's convert 1 5/16 back to an improper fraction:
-
Multiply the whole number by the denominator: 1 * 16 = 16
-
Add the numerator to the result: 16 + 5 = 21
-
Keep the denominator the same: The denominator remains 16.
-
Combine the results: The improper fraction is 21/16.
Working with Mixed Numbers: Addition, Subtraction, Multiplication, and Division
Performing arithmetic operations with mixed numbers often requires converting them to improper fractions first. Here's a brief overview:
Addition and Subtraction: Convert each mixed number to an improper fraction, find a common denominator, then add or subtract the numerators. Finally, convert the result back to a mixed number if necessary.
Multiplication and Division: You can either convert mixed numbers to improper fractions before performing the operation or multiply the whole numbers and fractions separately, then add them. The improper fraction method is generally easier for most people.
Common Mistakes to Avoid
-
Forgetting to convert: Many students forget to convert mixed numbers to improper fractions before adding, subtracting, multiplying or dividing. This leads to incorrect answers.
-
Incorrect order of operations: Always remember the order of operations (PEMDAS/BODMAS). Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
-
Incorrect simplification: Make sure to simplify fractions to their lowest terms after any operation.
Tips for Mastering Fraction Manipulation
-
Practice Regularly: The key to mastering fractions is consistent practice. Work through various problems, starting with simpler ones and gradually increasing the difficulty.
-
Use Visual Aids: Diagrams, charts, or physical manipulatives can help visualize fractions and make the concepts more concrete.
-
Seek Help When Needed: Don't hesitate to ask for help from teachers, tutors, or classmates if you encounter difficulties.
-
Utilize Online Resources: Many websites and apps offer interactive exercises and tutorials on fractions.
Beyond 21/16: Applying the Conversion Process to Other Improper Fractions
The method demonstrated for converting 21/16 applies to any improper fraction. Simply divide the numerator by the denominator, use the quotient as the whole number, the remainder as the new numerator, and keep the original denominator.
For example, to convert 37/8 to a mixed number:
37 ÷ 8 = 4 with a remainder of 5. Therefore, 37/8 = 4 5/8.
Conclusion
Converting 21/16 to a mixed number, and more broadly, understanding the manipulation of fractions, is a cornerstone of mathematical proficiency. This detailed guide provides not just the answer but also a deep dive into the underlying concepts, practical applications, and common pitfalls. With consistent practice and a clear understanding of the principles involved, mastering fraction manipulation will become second nature, opening doors to more advanced mathematical concepts and problem-solving skills. Remember the key steps: divide, use the quotient as the whole number, use the remainder as the numerator, and keep the same denominator. Good luck!
Latest Posts
Latest Posts
-
An Equation That Is Not A Linear Function
May 09, 2025
-
Division Of Fractions Worksheets With Answers Pdf
May 09, 2025
-
How Many 16 9 Fluid Ounces In A Gallon
May 09, 2025
-
4 X 3 2x And 10x
May 09, 2025
-
How Many Terms Are In The Expression Shown 2n 5 3p 4q
May 09, 2025
Related Post
Thank you for visiting our website which covers about 21 16 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.