50 Of What Number Is 15
News Co
May 08, 2025 · 4 min read
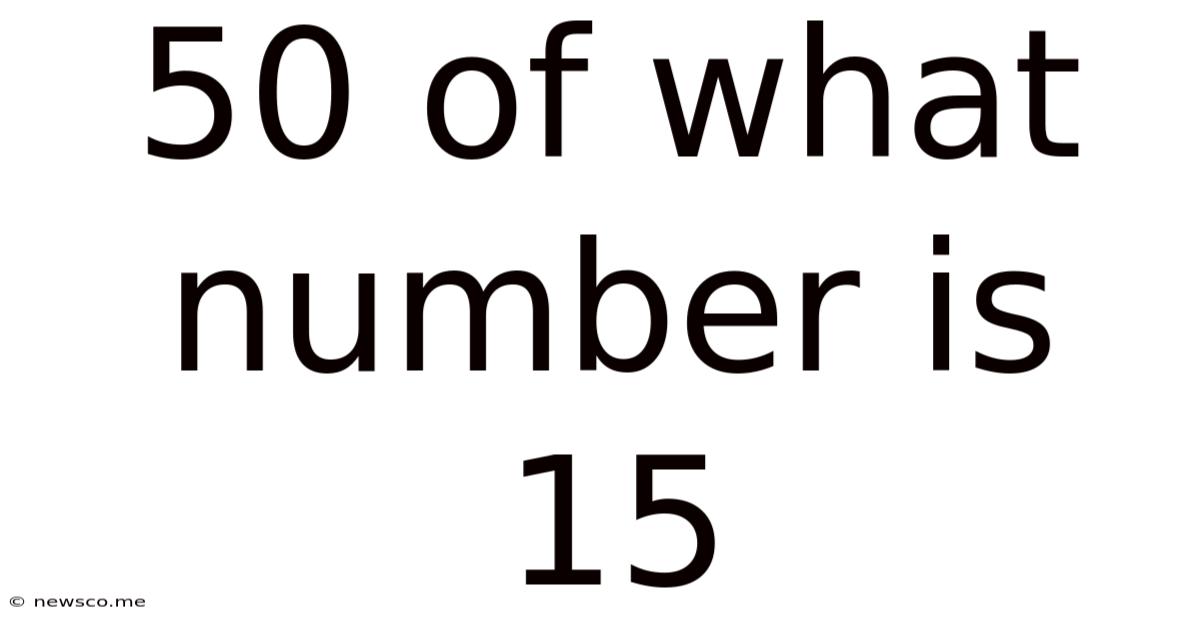
Table of Contents
50% of What Number is 15? Understanding Percentages and Solving Equations
Finding out what number 50% represents as 15 involves understanding percentages and solving simple algebraic equations. This seemingly simple question touches upon fundamental mathematical concepts crucial for various applications, from everyday budgeting to complex scientific calculations. Let's delve into the solution and explore the broader implications of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a part of 100. The symbol "%" represents "percent," meaning "out of one hundred." For example, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5. Understanding this fundamental concept is key to solving percentage problems.
Solving the Equation: 50% of What Number is 15?
The problem "50% of what number is 15?" can be translated into an algebraic equation. Let's represent the unknown number with the variable 'x'. The equation becomes:
0.5 * x = 15
This equation states that 50% (or 0.5) multiplied by an unknown number (x) equals 15. To solve for x, we need to isolate it on one side of the equation. We can do this by dividing both sides of the equation by 0.5:
x = 15 / 0.5
x = 30
Therefore, 50% of 30 is 15.
Different Approaches to Solving Percentage Problems
While the above method is straightforward, there are alternative approaches to solving percentage problems, each offering a unique perspective and potentially simplifying the calculation depending on the context. Let's explore some of these:
1. Using Proportions
Proportions offer a visual and intuitive way to solve percentage problems. We can set up a proportion as follows:
50/100 = 15/x
This proportion states that the ratio of 50 to 100 is equal to the ratio of 15 to the unknown number (x). Cross-multiplying, we get:
50x = 1500
Dividing both sides by 50:
x = 30
This method reinforces the concept of ratios and their equivalence in percentage problems.
2. Using the Percentage Formula
A general formula for percentage problems is:
(Percentage/100) * Whole = Part
In our problem:
(50/100) * x = 15
Solving for x, we again arrive at x = 30. This formula provides a structured approach applicable to a wide range of percentage calculations.
3. Mental Math Techniques
For simple percentages like 50%, mental math can be efficient. Since 50% is half, we can directly ask: "What number, when halved, equals 15?" The answer is immediately apparent: 30. This approach is particularly useful for quick estimations and everyday calculations.
Practical Applications of Percentage Calculations
The ability to solve percentage problems like "50% of what number is 15?" has wide-ranging applications in various fields:
1. Finance and Budgeting
Percentage calculations are fundamental in personal finance and business. Calculating discounts, interest rates, taxes, and profit margins all involve percentages. Understanding these calculations is crucial for making informed financial decisions. For example, if a store offers a 50% discount and an item costs $15 after the discount, you can use this method to determine the original price.
2. Science and Engineering
Percentages are used extensively in scientific research and engineering. Expressing experimental results, calculating error margins, and analyzing data often involve percentage calculations. For instance, determining the percentage of a certain element in a compound or calculating the efficiency of a machine involves percentage calculations.
3. Data Analysis and Statistics
Percentages are essential tools in data analysis and statistics. Representing data as percentages facilitates comparison and interpretation. For example, calculating the percentage of respondents who prefer a particular product in a survey, or the percentage change in a stock price over time, rely on percentage calculations.
4. Everyday Life
Percentages are encountered frequently in everyday situations. Calculating tips in restaurants, understanding sale prices, or figuring out the percentage of a task completed all involve percentage calculations. Mastering these calculations simplifies daily tasks and enhances decision-making.
Expanding on the Concept: Beyond 50%
While this article focused on "50% of what number is 15?", the principles discussed apply to any percentage problem. The key is to translate the word problem into an algebraic equation and then solve for the unknown variable. For instance, consider these related problems:
- 25% of what number is 15? This translates to 0.25x = 15, resulting in x = 60.
- 75% of what number is 15? This becomes 0.75x = 15, giving x = 20.
- 10% of what number is 15? This translates to 0.1x = 15, resulting in x = 150.
Solving these variations reinforces the understanding of percentage relationships and the adaptability of the equation-solving method.
Conclusion: Mastering Percentage Calculations
The question "50% of what number is 15?" serves as a gateway to understanding the broader world of percentage calculations. Mastering these calculations empowers you to confidently tackle various numerical challenges in diverse fields, from personal finance to scientific endeavors. By employing different approaches—algebraic equations, proportions, or mental math—you can choose the most efficient method depending on the complexity and context of the problem. Remember that practice is key to solidifying your understanding and developing proficiency in percentage calculations. The more you practice, the more intuitive and effortless these calculations will become.
Latest Posts
Latest Posts
-
What Are The Solutions Of X2 8 5x
May 09, 2025
-
Angle 1 And Angle 2 Form A Linear Pair
May 09, 2025
-
Lcm Of 7 4 And 2
May 09, 2025
-
How Many Lines Of Symmetry Does Isosceles Triangle Have
May 09, 2025
-
What Is The Graph Of 3x 5y 15
May 09, 2025
Related Post
Thank you for visiting our website which covers about 50 Of What Number Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.