Common Denominator Of 7 And 9
News Co
Apr 03, 2025 · 5 min read
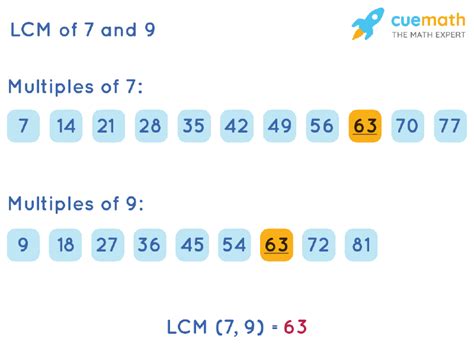
Table of Contents
Finding the Least Common Denominator (LCD) of 7 and 9: A Comprehensive Guide
Finding the least common denominator (LCD) of two numbers is a fundamental concept in mathematics, particularly crucial for adding or subtracting fractions. This article will delve deep into the process of determining the LCD of 7 and 9, exploring different methods and highlighting the underlying mathematical principles. We'll also examine the broader applications of LCDs and address common misconceptions.
Understanding Least Common Denominator (LCD)
Before diving into the specifics of 7 and 9, let's establish a solid understanding of the LCD. The least common denominator is the smallest number that is a multiple of both denominators. It's the smallest number that both denominators can divide into evenly. This is essential because adding or subtracting fractions requires them to have the same denominator. Without a common denominator, direct addition or subtraction isn't possible.
Why is the LCD Important?
The LCD is not simply a mathematical formality; it's a fundamental tool for performing arithmetic operations with fractions. Using the LCD ensures accuracy and simplifies calculations. Using a common denominator, but not the least common denominator, will lead to a correct answer, but it will require further simplification afterward, adding extra steps and potential for errors. The LCD provides the most efficient path to the solution.
Methods for Finding the LCD of 7 and 9
There are several methods to determine the LCD of 7 and 9. We'll explore the most common approaches:
1. Listing Multiples
This method is straightforward, particularly for smaller numbers. We simply list the multiples of each number until we find the smallest multiple that appears in both lists.
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90...
Notice that 63 appears in both lists. Therefore, the least common multiple (LCM) of 7 and 9 is 63. Since the LCD is the LCM of the denominators, the LCD of 7 and 9 is 63.
2. Prime Factorization
This method is particularly useful for larger numbers or when dealing with multiple denominators. It involves breaking down each number into its prime factors. A prime number is a number greater than 1 that has only two factors: 1 and itself.
- Prime factorization of 7: 7 (7 is a prime number)
- Prime factorization of 9: 3 x 3 = 3²
To find the LCM using prime factorization:
- Identify all the prime factors that appear in either factorization. In this case, we have 3 and 7.
- For each prime factor, take the highest power that appears in any factorization. The highest power of 3 is 3², and the highest power of 7 is 7¹.
- Multiply these highest powers together: 3² x 7 = 9 x 7 = 63
Therefore, the LCD of 7 and 9 is 63. This method is more efficient and less prone to errors than listing multiples, especially when working with larger numbers.
3. Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers without leaving a remainder.
- Find the GCD of 7 and 9: Since 7 and 9 share no common factors other than 1, their GCD is 1.
- Apply the formula: LCM(7, 9) = (|7 x 9|) / GCD(7, 9) = 63 / 1 = 63
Again, the LCD of 7 and 9 is 63. This formula provides a concise and elegant solution, particularly helpful when dealing with larger numbers where finding the GCD might be easier than listing multiples or performing prime factorization.
Practical Application: Adding Fractions
Let's demonstrate the practical application of finding the LCD of 7 and 9 by adding two fractions: 2/7 + 1/9.
-
Find the LCD: As we've established, the LCD of 7 and 9 is 63.
-
Convert the fractions to equivalent fractions with the LCD:
- 2/7 = (2 x 9) / (7 x 9) = 18/63
- 1/9 = (1 x 7) / (9 x 7) = 7/63
-
Add the fractions: 18/63 + 7/63 = 25/63
Therefore, 2/7 + 1/9 = 25/63. Without finding the LCD, this addition would not be possible.
Common Misconceptions about LCD
-
Simply multiplying the denominators: While multiplying the denominators will always result in a common denominator, it's not guaranteed to be the least common denominator. Using a larger common denominator necessitates simplification later, making the process less efficient.
-
LCD only applies to addition and subtraction: The concept of LCD is fundamental for working with fractions, and while its most immediate application is addition and subtraction, understanding LCD is crucial for other operations involving fractions as well.
-
LCD only works for two numbers: The principles of finding the LCD extend to situations involving more than two numbers. The methods outlined above, particularly prime factorization, can be easily adapted to find the LCD of three or more numbers.
Conclusion: Mastering the LCD
Finding the least common denominator is a vital skill in mathematics. Understanding the different methods—listing multiples, prime factorization, and using the GCD formula—empowers you to choose the most efficient approach based on the numbers involved. Mastering this concept is crucial not only for simplifying fraction arithmetic but also for building a solid foundation for more advanced mathematical concepts. Remember, the accuracy and efficiency of working with fractions depend heavily on a clear understanding and application of the LCD. Practice regularly to solidify your understanding and enhance your problem-solving skills. The seemingly simple task of finding the LCD for 7 and 9 actually opens the door to a much broader understanding of number theory and its practical applications.
Latest Posts
Latest Posts
-
How Much Is 9 Pounds In Us Dollars
Apr 04, 2025
-
What Percent Is 9 Out Of 20
Apr 04, 2025
-
How To Multiply Mixed Fractions And Whole Numbers
Apr 04, 2025
-
What Is The Least Common Factor Of 12 And 8
Apr 04, 2025
-
What Is 3 1 2 As An Improper Fraction
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Common Denominator Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
