What Is The Least Common Factor Of 12 And 8
News Co
Apr 04, 2025 · 5 min read
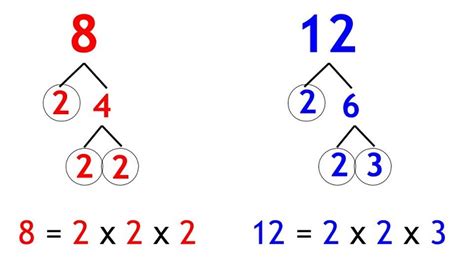
Table of Contents
What is the Least Common Factor of 12 and 8? A Deep Dive into Number Theory
Finding the least common factor (LCF) might seem like a simple task, especially for numbers like 12 and 8. However, understanding the underlying concepts of number theory involved unlocks a deeper appreciation of mathematics and its applications. This article will comprehensively explore the concept of LCF, focusing specifically on the example of 12 and 8, while also delving into related concepts such as prime factorization, greatest common divisor (GCD), and their significance in various fields. We'll even look at different methods for calculating the LCF, ensuring a thorough and accessible understanding for everyone.
Understanding Least Common Factor (LCF)
The least common factor (LCF), also known as the least common multiple (LCM), is the smallest positive integer that is a multiple of two or more integers. It's crucial to differentiate between the LCF and the greatest common divisor (GCD). The GCD is the largest positive integer that divides each of the integers without leaving a remainder. While seemingly opposites, the LCF and GCD are intrinsically linked, as we'll see later.
In our case, we want to find the LCF of 12 and 8. This means we're looking for the smallest positive integer that is divisible by both 12 and 8 without leaving a remainder.
Method 1: Listing Multiples
A straightforward, albeit sometimes lengthy method, is listing the multiples of each number until a common multiple is found.
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ...
- Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, ...
By comparing the lists, we observe that 24, 48, 72, 96, and 120 are common multiples. The smallest of these is 24. Therefore, the LCF of 12 and 8 is 24.
Method 2: Prime Factorization
This method is more efficient, especially for larger numbers. It leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers.
-
Find the prime factorization of each number:
- 12 = 2 x 2 x 3 = 2² x 3
- 8 = 2 x 2 x 2 = 2³
-
Identify the highest power of each prime factor present in either factorization:
- The prime factors are 2 and 3.
- The highest power of 2 is 2³ = 8.
- The highest power of 3 is 3¹ = 3.
-
Multiply the highest powers together:
- LCF(12, 8) = 2³ x 3 = 8 x 3 = 24
This method offers a more systematic approach, avoiding the need to list out numerous multiples.
Method 3: Using the GCD
The relationship between the LCF (LCM) and the GCD is elegantly expressed by the following formula:
LCF(a, b) = (|a x b|) / GCD(a, b)
where:
- a and b are the two integers.
- |a x b| represents the absolute value of the product of a and b.
- GCD(a, b) is the greatest common divisor of a and b.
First, we need to find the GCD of 12 and 8. We can use the Euclidean algorithm for this:
- Divide the larger number (12) by the smaller number (8): 12 ÷ 8 = 1 with a remainder of 4.
- Replace the larger number with the smaller number (8) and the smaller number with the remainder (4): 8 ÷ 4 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 4. Therefore, GCD(12, 8) = 4.
Now, we can apply the formula:
LCF(12, 8) = (|12 x 8|) / GCD(12, 8) = 96 / 4 = 24
The Significance of LCF and GCD
The concepts of LCF and GCD extend far beyond simple arithmetic exercises. They have significant applications in various fields:
1. Scheduling and Time Management:
Imagine two buses that depart from the same station, but one leaves every 12 minutes and the other every 8 minutes. Finding the LCF helps determine when both buses will depart simultaneously again. The answer is 24 minutes.
2. Fraction Arithmetic:
When adding or subtracting fractions, finding the LCF of the denominators is crucial for obtaining a common denominator.
3. Modular Arithmetic and Cryptography:
LCF and GCD play a fundamental role in modular arithmetic, a branch of number theory with applications in cryptography and computer science. Algorithms like the Euclidean algorithm are essential for efficient computations in these fields.
4. Music Theory:
In music, understanding harmonic intervals often involves concepts related to LCF and GCD.
Further Exploration: Advanced Concepts
This section briefly touches upon more advanced concepts related to LCF and GCD:
- Least Common Multiple (LCM) of more than two numbers: The principles discussed can be extended to find the LCM of three or more integers.
- Euclidean Algorithm and its efficiency: The Euclidean algorithm provides an efficient method for computing the GCD, even for very large numbers. Its efficiency is crucial in various applications.
- Applications in Abstract Algebra: The concepts of GCD and LCM extend to more abstract algebraic structures, showcasing their fundamental importance in mathematics.
Conclusion
Finding the least common factor of 12 and 8, while seemingly a simple problem, provides a gateway to understanding fundamental concepts within number theory. We explored three distinct methods – listing multiples, prime factorization, and utilizing the GCD – highlighting the interconnectedness of these mathematical concepts. The widespread applications of LCF and GCD in various fields underscore their importance beyond simple arithmetic, solidifying their place as essential tools in mathematics and beyond. Whether you're a student grappling with number theory or a professional needing to apply these concepts, understanding LCF and GCD offers a powerful advantage in problem-solving and analytical thinking. The journey from a simple problem like finding the LCF of 12 and 8 to grasping the wider mathematical landscape is a testament to the beauty and power of mathematical principles.
Latest Posts
Latest Posts
-
All Squares Are Rectangles True Or False
Apr 04, 2025
-
How To Find A 90 Confidence Interval
Apr 04, 2025
-
How Do You Find The Height Of An Isosceles Triangle
Apr 04, 2025
-
What Is The Lcm For 5 And 6
Apr 04, 2025
-
Are Same Side Interior Angles Supplementary
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Least Common Factor Of 12 And 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
