What Is 3 1/2 As An Improper Fraction
News Co
Apr 04, 2025 · 5 min read
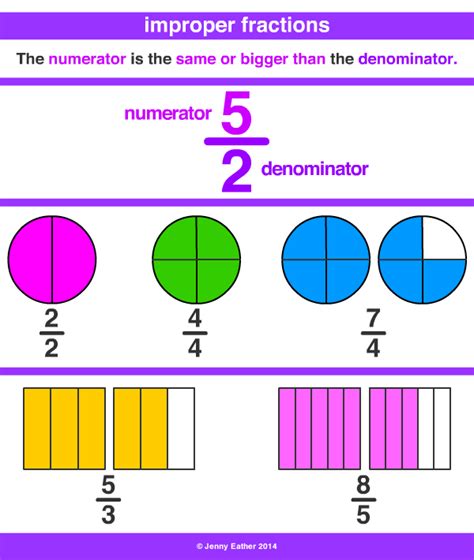
Table of Contents
What is 3 1/2 as an Improper Fraction? A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, crucial for various applications from basic arithmetic to advanced calculus. This article delves deep into the conversion of mixed numbers, like 3 1/2, into improper fractions, explaining the process, the reasons behind it, and offering practical examples to solidify your understanding.
Understanding Mixed Numbers and Improper Fractions
Before diving into the conversion process, let's define our key terms:
Mixed Number: A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator (top number) smaller than its denominator (bottom number). For example, 3 1/2 is a mixed number; 3 is the whole number, and 1/2 is the proper fraction.
Improper Fraction: An improper fraction has a numerator that is greater than or equal to its denominator. For instance, 7/2 is an improper fraction because the numerator (7) is larger than the denominator (2).
The key difference lies in how they represent quantities. A mixed number represents a whole quantity plus a part of a whole, while an improper fraction represents a quantity greater than one whole expressed as a single fraction. Both represent the same value, just in different formats.
Converting 3 1/2 to an Improper Fraction: The Step-by-Step Process
The conversion of 3 1/2 to an improper fraction involves a simple two-step process:
Step 1: Multiply the whole number by the denominator.
In our example, the whole number is 3, and the denominator of the fraction is 2. Therefore, we multiply 3 * 2 = 6.
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 1. Adding this to the result from Step 1, we get 6 + 1 = 7.
Step 3: Keep the denominator the same.
The denominator remains unchanged throughout the conversion. Therefore, the denominator remains 2.
Step 4: Combine the results to form the improper fraction.
Combining the results, we get the improper fraction 7/2. This means that 3 1/2 is equivalent to 7/2.
Why Convert Mixed Numbers to Improper Fractions?
The conversion of mixed numbers to improper fractions is crucial in various mathematical operations, primarily because it simplifies calculations involving fractions. Here's why:
-
Simplification of Arithmetic Operations: Performing arithmetic operations (addition, subtraction, multiplication, and division) with improper fractions is often easier and more straightforward than with mixed numbers. It eliminates the need for separate operations on the whole number and fractional parts, streamlining the calculation process.
-
Consistency in Calculations: Using improper fractions ensures consistency in calculations, particularly when dealing with multiple fractions in an equation. This consistency reduces the chances of errors and facilitates easier understanding and interpretation of the results.
-
Solving Equations: In many algebraic equations, especially those involving fractions, it's often necessary to express all terms as improper fractions to simplify the equation and solve for the unknown variable.
-
Advanced Mathematical Concepts: The concept of improper fractions is essential for understanding more advanced mathematical concepts, such as rational numbers, complex numbers, and calculus. A firm grasp of this fundamental concept lays a strong foundation for future mathematical studies.
Real-World Applications of Improper Fractions
Improper fractions aren't just abstract mathematical concepts; they have practical applications in various real-world scenarios. Here are a few examples:
-
Baking and Cooking: Recipes often use fractions to represent ingredients. Converting mixed numbers to improper fractions can simplify calculations when scaling a recipe up or down. For example, if a recipe calls for 3 1/2 cups of flour, representing it as 7/2 makes it easier to double or halve the recipe.
-
Construction and Engineering: Construction and engineering projects frequently involve precise measurements and calculations. Improper fractions provide a more accurate and efficient way to represent and calculate measurements, reducing the likelihood of errors.
-
Finance and Accounting: Improper fractions can be used to represent financial ratios and proportions, facilitating calculations in financial planning, analysis, and decision-making.
-
Data Analysis and Statistics: Data analysis and statistics often involve handling fractions to represent proportions and probabilities. Improper fractions can be a useful tool for such calculations.
More Examples of Converting Mixed Numbers to Improper Fractions
Let's practice converting more mixed numbers to improper fractions to reinforce the understanding of the process:
-
Convert 2 3/4 to an improper fraction:
- Multiply the whole number by the denominator: 2 * 4 = 8
- Add the numerator: 8 + 3 = 11
- Keep the denominator: 4
- Result: 11/4
-
Convert 5 1/3 to an improper fraction:
- Multiply the whole number by the denominator: 5 * 3 = 15
- Add the numerator: 15 + 1 = 16
- Keep the denominator: 3
- Result: 16/3
-
Convert 1 7/8 to an improper fraction:
- Multiply the whole number by the denominator: 1 * 8 = 8
- Add the numerator: 8 + 7 = 15
- Keep the denominator: 8
- Result: 15/8
-
Convert 4 2/5 to an improper fraction:
- Multiply the whole number by the denominator: 4 * 5 = 20
- Add the numerator: 20 + 2 = 22
- Keep the denominator: 5
- Result: 22/5
Converting Improper Fractions Back to Mixed Numbers
It's equally important to understand the reverse process – converting improper fractions back to mixed numbers. This involves dividing the numerator by the denominator. The quotient becomes the whole number, the remainder becomes the numerator, and the denominator remains the same.
For example, converting 7/2 back to a mixed number:
- Divide 7 by 2: 7 ÷ 2 = 3 with a remainder of 1.
- The quotient (3) is the whole number.
- The remainder (1) is the new numerator.
- The denominator remains 2.
- Result: 3 1/2
Conclusion: Mastering the Art of Fraction Conversion
Converting mixed numbers to improper fractions is a fundamental skill in mathematics, facilitating easier and more efficient calculations. Understanding this process and its applications is crucial for success in various mathematical and real-world contexts. By mastering this skill, you enhance your problem-solving abilities and build a solid foundation for more advanced mathematical concepts. Remember the simple steps, practice regularly with diverse examples, and you'll quickly become proficient in converting between mixed numbers and improper fractions.
Latest Posts
Latest Posts
-
What Is The Least Common Multiple Of 3 2
Apr 04, 2025
-
Least Common Multiple Of 6 7 And 8
Apr 04, 2025
-
All Squares Are Rectangles True Or False
Apr 04, 2025
-
How To Find A 90 Confidence Interval
Apr 04, 2025
-
How Do You Find The Height Of An Isosceles Triangle
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 1/2 As An Improper Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
