Domain And Range Of An Absolute Value Function
News Co
Apr 05, 2025 · 6 min read
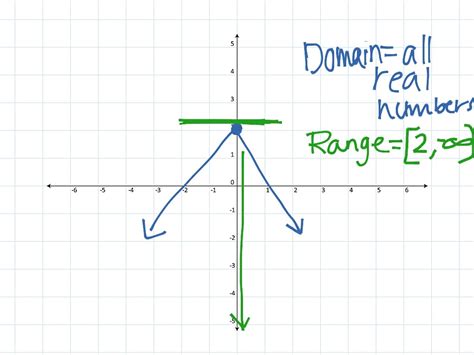
Table of Contents
Domain and Range of an Absolute Value Function: A Comprehensive Guide
Understanding the domain and range of functions is crucial in algebra and precalculus. This comprehensive guide will delve into the specifics of determining the domain and range of absolute value functions, providing clear explanations, examples, and helpful tips to solidify your understanding. We will explore different forms of absolute value functions and how their transformations affect the domain and range.
What are Domain and Range?
Before we dive into the intricacies of absolute value functions, let's establish a solid foundation by defining domain and range:
-
Domain: The domain of a function represents all possible input values (x-values) for which the function is defined. Essentially, it's the set of all x-values that produce a real output (y-value).
-
Range: The range of a function encompasses all possible output values (y-values) that the function can generate. It's the set of all y-values that result from the defined input values.
Understanding Absolute Value Functions
An absolute value function is a function that contains an absolute value expression. The absolute value of a number is its distance from zero, always resulting in a non-negative value. The standard form of an absolute value function is:
f(x) = |x|
This function returns the positive value of x, regardless of whether x is positive or negative. For example:
- |5| = 5
- |-5| = 5
Determining the Domain of an Absolute Value Function
The beauty of absolute value functions lies in their simplicity when it comes to determining their domain. The domain of a basic absolute value function, f(x) = |x|, is all real numbers. This is because you can substitute any real number for x, and the function will always produce a defined real output. This is represented in interval notation as:
(-∞, ∞)
Domain of Transformed Absolute Value Functions
More complex absolute value functions may involve transformations such as shifts, stretches, and reflections. However, these transformations do not alter the domain. Consider the following examples:
-
f(x) = |x + 3|: This function shifts the basic absolute value function three units to the left. The domain remains (-∞, ∞).
-
f(x) = |x| - 5: This function shifts the basic absolute value function five units down. The domain remains (-∞, ∞).
-
f(x) = 2|x - 1| + 4: This function involves a vertical stretch by a factor of 2, a horizontal shift one unit to the right, and a vertical shift four units up. The domain is still (-∞, ∞).
In essence, unless the absolute value function is combined with another function that restricts the domain (like a fraction with x in the denominator or a square root), the domain of an absolute value function will always be all real numbers.
Determining the Range of an Absolute Value Function
Determining the range of an absolute value function requires a bit more attention than determining the domain. Let's start with the basic function:
Range of the Basic Absolute Value Function
The range of the basic absolute value function, f(x) = |x|, is [0, ∞). This is because the absolute value of any number is always greater than or equal to zero. The function will never produce a negative y-value.
Range of Transformed Absolute Value Functions
Transformations significantly affect the range of an absolute value function. Let's analyze how different transformations alter the range:
-
Vertical Shifts: A vertical shift (adding or subtracting a constant outside the absolute value) shifts the entire graph up or down. For example:
- f(x) = |x| + 2: The range is [2, ∞). The graph is shifted up by two units.
- f(x) = |x| - 4: The range is [-4, ∞). The graph is shifted down by four units.
-
Vertical Stretches and Compressions: A vertical stretch or compression (multiplying the absolute value expression by a constant) affects the steepness of the graph but doesn't change the minimum y-value.
- f(x) = 3|x|: The range is [0, ∞). The graph is stretched vertically.
- f(x) = (1/2)|x|: The range is [0, ∞). The graph is compressed vertically.
-
Horizontal Shifts: Horizontal shifts (adding or subtracting a constant inside the absolute value) do not affect the range. The minimum y-value remains unchanged.
-
Reflections: A reflection across the x-axis (multiplying the entire function by -1) changes the range to (-∞, 0]. A reflection across the y-axis (negating x inside the absolute value) doesn't affect the range because |-x| = |x|.
To find the range of a transformed absolute value function, consider the vertex of the graph. The y-coordinate of the vertex represents the minimum or maximum y-value (depending on whether there's a reflection). The range will extend from this minimum/maximum value to positive or negative infinity, depending on the reflection and vertical shifts.
Examples of Finding Domain and Range
Let's work through some examples to solidify our understanding:
Example 1:
Find the domain and range of f(x) = |x - 2| + 1.
-
Domain: The domain is (-∞, ∞) since there are no restrictions on the input values.
-
Range: The vertex of this function is (2, 1). Since the absolute value function opens upwards, the minimum y-value is 1. Therefore, the range is [1, ∞).
Example 2:
Find the domain and range of f(x) = -|x + 4| - 3.
-
Domain: The domain is (-∞, ∞).
-
Range: The vertex is (-4, -3). The negative sign in front of the absolute value reflects the graph across the x-axis, making the vertex a maximum. Therefore, the range is (-∞, -3].
Example 3:
Find the domain and range of f(x) = 2|x + 1| - 5
-
Domain: The domain is (-∞, ∞).
-
Range: The vertex is (-1, -5). The function opens upwards. Therefore, the range is [-5, ∞).
Piecewise Definition and Absolute Value
It's often helpful to understand the piecewise definition of the absolute value function. This can make it easier to visualize and work with absolute value functions, especially when dealing with more complex expressions. The piecewise definition of the absolute value function is:
|x| = x, if x ≥ 0
-x, if x < 0
This means that the absolute value function behaves differently depending on whether the input is positive or negative. This definition can be used to solve equations and inequalities involving absolute values and to better understand the behavior of the function for different intervals of x.
Using the piecewise definition, you can rewrite transformed absolute value functions as piecewise functions to further solidify your understanding of their domains and ranges.
Conclusion
Understanding the domain and range of absolute value functions is a fundamental concept in mathematics. While the domain is consistently all real numbers for standard absolute value functions, the range depends heavily on transformations such as shifts, stretches, reflections, and combinations with other functions. By mastering the techniques and examples outlined in this guide, you can confidently determine the domain and range of any absolute value function you encounter. Remember to always consider the vertex of the graph and the impact of transformations on its position and orientation. Using the piecewise definition can also provide valuable insights and enhance your problem-solving abilities. Practice regularly, and you will master this essential concept in function analysis.
Latest Posts
Latest Posts
-
Lowest Common Multiple Of 12 And 24
Apr 05, 2025
-
What Is An Equivalent Fraction For 2 3
Apr 05, 2025
-
Whats The Greatest Common Factor Of 8 And 12
Apr 05, 2025
-
150 Square Meters In Square Feet
Apr 05, 2025
-
0 1 To The Power Of 3
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Domain And Range Of An Absolute Value Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
