How Do You Find Area Of A Scalene Triangle
News Co
Apr 02, 2025 · 7 min read
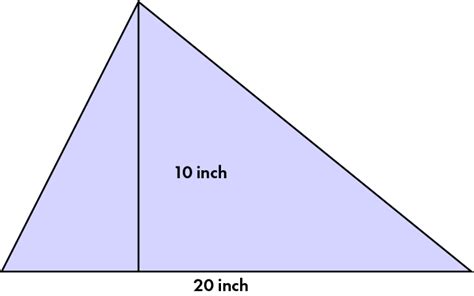
Table of Contents
How to Find the Area of a Scalene Triangle: A Comprehensive Guide
Finding the area of a triangle is a fundamental concept in geometry, with applications ranging from simple land surveying to complex engineering calculations. While the formula for the area of a right-angled triangle (½ * base * height) is straightforward, calculating the area of a scalene triangle—a triangle with three unequal sides—requires a slightly more nuanced approach. This comprehensive guide will explore several methods for determining the area of a scalene triangle, equipping you with the knowledge and tools to tackle this geometrical challenge effectively. We'll cover everything from the basic Heron's formula to more advanced techniques, ensuring you have a complete understanding of this important topic.
Understanding Scalene Triangles
Before diving into the area calculations, let's solidify our understanding of what constitutes a scalene triangle. A scalene triangle is defined as a triangle with three sides of different lengths and, consequently, three angles of different measures. Unlike isosceles triangles (two equal sides) or equilateral triangles (three equal sides), scalene triangles lack symmetry, making the area calculation slightly more involved.
This lack of symmetry is precisely what necessitates the use of different formulas and techniques compared to simpler triangles. We cannot simply use the base and height directly unless we're already provided with the height. We often need to derive the height or employ alternative methods.
Method 1: Heron's Formula – The Classic Approach
Heron's formula is a remarkably elegant and widely used method for calculating the area of any triangle, including scalene triangles, when the lengths of all three sides are known. It's a powerful tool because it bypasses the need to explicitly calculate the height of the triangle.
The Formula:
Area = √[s(s-a)(s-b)(s-c)]
Where:
- a, b, and c are the lengths of the three sides of the triangle.
- s is the semi-perimeter of the triangle, calculated as s = (a + b + c) / 2
Step-by-Step Calculation:
- Find the semi-perimeter (s): Add the lengths of all three sides (a, b, c) and divide the sum by 2.
- Apply Heron's formula: Substitute the values of s, a, b, and c into the formula.
- Calculate the area: Evaluate the expression under the square root to obtain the area of the triangle.
Example:
Let's say we have a scalene triangle with sides a = 5 cm, b = 6 cm, and c = 7 cm.
- Semi-perimeter (s): s = (5 + 6 + 7) / 2 = 9 cm
- Heron's formula: Area = √[9(9-5)(9-6)(9-7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm²
Therefore, the area of the scalene triangle is approximately 14.7 square centimeters.
Method 2: Using Trigonometry – The Sine Rule Approach
Trigonometry provides another powerful method for finding the area of a scalene triangle, especially when you know the length of two sides and the angle between them. This method leverages the sine function to directly calculate the area.
The Formula:
Area = (1/2) * a * b * sin(C)
Where:
- a and b are the lengths of two sides of the triangle.
- C is the angle between sides a and b.
Step-by-Step Calculation:
- Identify the known values: You need the lengths of two sides (a and b) and the angle (C) between them.
- Apply the formula: Substitute the values into the formula. Remember to ensure your calculator is set to the correct angle mode (degrees or radians).
- Calculate the area: Evaluate the expression to obtain the area of the triangle.
Example:
Consider a scalene triangle with sides a = 8 cm and b = 10 cm, and the angle C between them is 60 degrees.
- Known values: a = 8 cm, b = 10 cm, C = 60°
- Trigonometric formula: Area = (1/2) * 8 * 10 * sin(60°) = 40 * (√3/2) ≈ 34.64 cm²
The area of the scalene triangle is approximately 34.64 square centimeters.
Method 3: Dividing into Right-Angled Triangles – A Geometric Approach
This method involves dividing the scalene triangle into two right-angled triangles. This requires knowing at least one side length and the height of the triangle.
Step-by-Step Calculation:
- Draw an altitude: Draw a perpendicular line from one vertex to the opposite side (base), creating two right-angled triangles. This line is the height (h) of the original triangle.
- Calculate the height (h): Use trigonometric functions (sine or cosine) or the Pythagorean theorem if you know enough information about the right-angled triangles.
- Calculate the area of each right-angled triangle: Area = (1/2) * base * height. For each of the smaller triangles, use the appropriate base segment and the height (h) you calculated.
- Sum the areas: Add the areas of the two right-angled triangles to find the total area of the original scalene triangle.
Example:
Let's assume a scalene triangle has a base of 12 cm and a height of 7 cm.
- Height: h = 7 cm (already given)
- Area of each smaller triangle is 1/2base segmentheight If the altitude splits the base into segments of 4 cm and 8 cm, then the areas would be (1/2)(4)(7) = 14 cm² and (1/2)(8)(7) = 28 cm².
- Sum: 14 cm² + 28 cm² = 42 cm²
Therefore, the area of the scalene triangle is 42 square centimeters. This is a simpler calculation when you have the base and height directly.
Method 4: Coordinate Geometry – For Advanced Applications
If the vertices of the scalene triangle are given as coordinates in a Cartesian plane (x, y), you can utilize the determinant method from coordinate geometry. This method is particularly useful when dealing with triangles defined by their vertices rather than their side lengths.
The Formula:
Area = (1/2) |(x₁ (y₂ - y₃) + x₂ (y₃ - y₁) + x₃ (y₁ - y₂))|
Where:
- (x₁, y₁), (x₂, y₂), and (x₃, y₃) are the coordinates of the three vertices.
Step-by-Step Calculation:
- Label the coordinates: Assign coordinates (x₁, y₁), (x₂, y₂), and (x₃, y₃) to the three vertices of the triangle.
- Apply the determinant formula: Substitute the coordinates into the formula. The absolute value ensures a positive area.
- Calculate the area: Evaluate the expression to obtain the area of the triangle.
Example:
Let's say the vertices of a scalene triangle are A(1, 2), B(4, 6), and C(7, 3).
- Coordinates: (x₁, y₁) = (1, 2), (x₂, y₂) = (4, 6), (x₃, y₃) = (7, 3)
- Determinant formula: Area = (1/2) |(1(6-3) + 4(3-2) + 7(2-6))| = (1/2) |(3 + 4 - 28)| = (1/2) |-21| = 10.5 square units.
Therefore, the area of this scalene triangle is 10.5 square units.
Choosing the Right Method
The best method for calculating the area of a scalene triangle depends on the information available.
- Heron's formula: Ideal when you know the lengths of all three sides.
- Trigonometric method: Best when you have two sides and the angle between them.
- Right-angled triangle division: Useful if you can easily construct the altitude and know the base and height.
- Coordinate geometry: Essential when the vertices are expressed as coordinates.
Conclusion
Calculating the area of a scalene triangle might seem daunting initially, but with a clear understanding of the different methods available, it becomes a straightforward process. Remember to choose the most efficient approach based on the given information, whether it's the lengths of sides, angles, or coordinates. Mastering these techniques will significantly enhance your problem-solving skills in geometry and related fields. By understanding the intricacies of each method, you can confidently tackle diverse geometrical challenges and unlock a deeper appreciation for the elegance and practicality of mathematics. Remember to always double-check your calculations and consider using different methods to verify your results.
Latest Posts
Latest Posts
-
What Is The Prime Factorization Of 260
Apr 03, 2025
-
What Is The Greatest Common Factor Of 42 And 48
Apr 03, 2025
-
Mark The Integers On The Number Line
Apr 03, 2025
-
1 Cubic Meter Is How Many Cubic Centimeters
Apr 03, 2025
-
How To Convert A Mixed Fraction To A Whole Number
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about How Do You Find Area Of A Scalene Triangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
