Sum Of The Interior Angles Of A Nonagon
News Co
Apr 04, 2025 · 5 min read
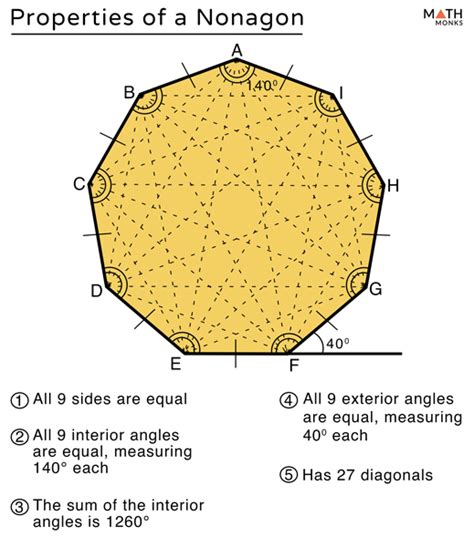
Table of Contents
Sum of the Interior Angles of a Nonagon: A Comprehensive Guide
The nonagon, a captivating polygon with nine sides and nine angles, presents a fascinating exploration into the world of geometry. Understanding the sum of its interior angles is crucial for various applications in mathematics, engineering, and design. This comprehensive guide delves into the calculation, properties, and applications of the sum of interior angles of a nonagon, offering a detailed explanation for both beginners and those seeking a deeper understanding.
Understanding Polygons: A Foundation
Before we dive into the specifics of nonagons, let's establish a foundational understanding of polygons. A polygon is a closed two-dimensional figure formed by connecting a series of straight line segments. These segments are called sides, and the points where the sides meet are called vertices. Polygons are classified based on the number of sides they possess:
- Triangle: 3 sides
- Quadrilateral: 4 sides
- Pentagon: 5 sides
- Hexagon: 6 sides
- Heptagon: 7 sides
- Octagon: 8 sides
- Nonagon: 9 sides
- Decagon: 10 sides
- And so on...
The sum of the interior angles of a polygon is directly related to the number of sides it possesses. This relationship provides a powerful tool for solving problems involving polygons of any number of sides.
Calculating the Sum of Interior Angles: The Formula
The sum of the interior angles of any polygon can be calculated using a simple formula. This formula is derived from the concept of dividing a polygon into triangles. Consider a polygon with n sides. You can always divide this polygon into (n-2) triangles by drawing diagonals from a single vertex. Since the sum of the angles in a single triangle is always 180 degrees, the sum of the interior angles of the polygon is (n-2) times 180 degrees.
Therefore, the formula for the sum of interior angles of a polygon with n sides is:
(n - 2) * 180°
Applying the Formula to a Nonagon
A nonagon, having nine sides (n=9), allows us to apply this formula directly. Substituting n=9 into the formula, we get:
(9 - 2) * 180° = 7 * 180° = 1260°
Therefore, the sum of the interior angles of a nonagon is 1260 degrees. This is a fundamental property of all nonagons, regardless of their shape or size. Whether it's a regular nonagon (with all sides and angles equal) or an irregular nonagon, the sum of its interior angles will always be 1260 degrees.
Regular vs. Irregular Nonagons: A Key Distinction
It's important to differentiate between regular and irregular nonagons.
-
Regular Nonagon: A regular nonagon has all nine sides of equal length and all nine angles of equal measure. Each interior angle of a regular nonagon measures 1260°/9 = 140°.
-
Irregular Nonagon: An irregular nonagon, on the other hand, has sides and angles of varying lengths and measures. While the sum of its interior angles remains 1260°, the individual angles will not all be equal to 140°.
This distinction is crucial when working with specific problems involving nonagons. The properties of a regular nonagon are more predictable and easier to work with, while irregular nonagons require a more case-by-case approach.
Practical Applications of Nonagon Geometry
Understanding the properties of nonagons, particularly the sum of their interior angles, has several practical applications across various fields:
1. Architecture and Design:
Nonagons can be found in architectural designs, often incorporated into building structures or decorative elements. Knowing the sum of interior angles is essential for accurately calculating angles and ensuring structural integrity. For instance, designing a nine-sided gazebo requires precise angular calculations to ensure proper construction.
2. Engineering:
In engineering, nonagons may appear in various mechanical designs. For example, the design of certain gears or components might involve nonagonal shapes, necessitating accurate angle calculations to ensure smooth operation and functionality. Understanding the sum of interior angles plays a vital role in such applications.
3. Computer Graphics and Game Development:
In computer graphics and game development, polygons, including nonagons, are used extensively to create models and shapes. The ability to calculate the interior angles accurately is crucial for rendering realistic and accurate 3D models. Games often feature many complex shapes, and understanding fundamental geometric principles like the sum of interior angles is essential for efficient design and rendering.
4. Tessellations and Art:
Nonagons can be used in creating tessellations, which are repeated patterns that cover a plane without any gaps or overlaps. Understanding the angular properties of nonagons helps in creating aesthetically pleasing and mathematically accurate tessellations. This has applications in art, design, and even flooring patterns.
Advanced Concepts and Further Exploration
For those interested in a deeper understanding, we can explore more advanced concepts:
1. Exterior Angles:
The sum of the exterior angles of any polygon, including a nonagon, is always 360°. This is an independent property that holds true regardless of the number of sides.
2. Interior Angle Relationships in Irregular Nonagons:
While the sum of interior angles in an irregular nonagon is always 1260°, the individual angles can vary significantly. Solving problems involving irregular nonagons often requires using other geometric principles and properties.
3. Nonagon-based constructions:
Understanding the properties of nonagons leads to an exploration of various geometric constructions involving nonagons. These constructions often require a solid grasp of angular relationships and the use of geometric tools like compasses and rulers.
Conclusion: The Significance of Understanding Nonagon Geometry
Understanding the sum of the interior angles of a nonagon is a fundamental concept in geometry with far-reaching applications. From architectural design to computer graphics, the ability to calculate and utilize angular properties is crucial for various problem-solving scenarios. This guide has provided a comprehensive overview of this important geometric principle, helping readers grasp its significance and application across multiple disciplines. By understanding this foundational concept, one can further explore the fascinating world of geometry and its endless possibilities. The 1260° sum of interior angles serves as a cornerstone for many more complex geometric explorations. This knowledge equips you with the essential tools to tackle various challenges involving nine-sided polygons in a wide range of applications.
Latest Posts
Latest Posts
-
How Many Sides Do A Octagon Have
Apr 05, 2025
-
What Is 59 In Roman Numerals
Apr 05, 2025
-
Is 81 A Prime Number Or A Composite Number
Apr 05, 2025
-
What Is 20 C In F
Apr 05, 2025
-
Solving For B In Y Mx B
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Sum Of The Interior Angles Of A Nonagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
