Solving For B In Y Mx B
News Co
Apr 05, 2025 · 5 min read
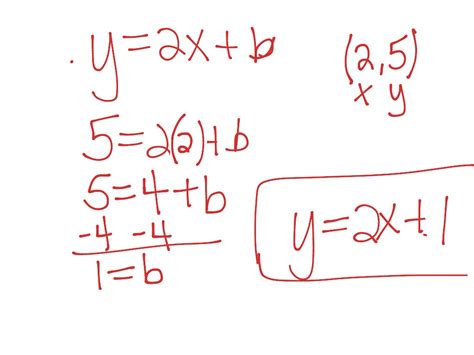
Table of Contents
Solving for b in y = mx + b: A Comprehensive Guide
The equation y = mx + b represents a fundamental concept in algebra and is the slope-intercept form of a linear equation. Understanding how to manipulate this equation, particularly solving for 'b', is crucial for various applications, from simple graphing to complex data analysis. This comprehensive guide will break down the process of solving for 'b' in detail, exploring different scenarios and providing practical examples.
Understanding the Equation: y = mx + b
Before diving into solving for 'b', let's refresh our understanding of the equation itself. Each component holds significance:
-
y: Represents the dependent variable. Its value depends on the value of x. Think of y as the output or result.
-
m: Represents the slope of the line. The slope describes the steepness and direction of the line. A positive slope indicates an upward trend, while a negative slope indicates a downward trend. A slope of zero represents a horizontal line.
-
x: Represents the independent variable. This is the input value that determines the value of y.
-
b: Represents the y-intercept. This is the point where the line intersects the y-axis (where x = 0). It's the value of y when x is zero.
Solving for b: The Basic Steps
To solve for 'b', we need to isolate it on one side of the equation. This involves performing inverse operations to move the other terms to the opposite side. Here's the step-by-step process:
-
Start with the equation: y = mx + b
-
Subtract mx from both sides: This cancels out the 'mx' term on the right side, leaving 'b' isolated. The equation becomes: y - mx = b
-
Rearrange the equation (optional): For clarity, you can rearrange the equation to have 'b' on the left side: b = y - mx
Practical Examples: Solving for b with Given Values
Let's solidify our understanding with some practical examples. We'll be given values for 'y', 'm', and 'x', and we'll solve for 'b'.
Example 1:
Given: y = 5, m = 2, x = 3
-
Substitute the values into the equation: 5 = 2(3) + b
-
Simplify: 5 = 6 + b
-
Subtract 6 from both sides: -1 = b
Therefore, b = -1
Example 2:
Given: y = -4, m = -1, x = 2
-
Substitute the values into the equation: -4 = -1(2) + b
-
Simplify: -4 = -2 + b
-
Add 2 to both sides: -2 = b
Therefore, b = -2
Example 3:
Given: y = 0, m = 3, x = -1
-
Substitute the values into the equation: 0 = 3(-1) + b
-
Simplify: 0 = -3 + b
-
Add 3 to both sides: 3 = b
Therefore, b = 3
Solving for b when dealing with Fractions and Decimals
The process remains the same even when dealing with fractions or decimals. Just ensure you carefully handle the arithmetic operations.
Example 4 (Fractions):
Given: y = 1/2, m = 1/4, x = 2
-
Substitute the values: 1/2 = (1/4)(2) + b
-
Simplify: 1/2 = 1/2 + b
-
Subtract 1/2 from both sides: 0 = b
Therefore, b = 0
Example 5 (Decimals):
Given: y = 2.5, m = 1.5, x = 1
-
Substitute the values: 2.5 = 1.5(1) + b
-
Simplify: 2.5 = 1.5 + b
-
Subtract 1.5 from both sides: 1 = b
Therefore, b = 1
Real-World Applications of Solving for b
Solving for 'b' is not just an academic exercise; it has practical applications in various fields:
-
Economics: In linear demand and supply models, 'b' represents the y-intercept, which can indicate the quantity demanded or supplied even at a zero price.
-
Physics: In physics, linear equations are used to model motion and other physical phenomena. Solving for 'b' can help determine initial conditions or starting points.
-
Engineering: Linear equations are extensively used in engineering design and analysis. Solving for 'b' can be essential in determining parameters such as initial displacement or starting voltage.
-
Data Analysis: When fitting a linear regression model to data, the y-intercept ('b') provides valuable insights into the relationship between variables.
Advanced Scenarios and Considerations
While the basic process remains consistent, some scenarios require additional steps or considerations:
-
Solving for b when only two points are given: If you're given two points (x1, y1) and (x2, y2) instead of 'm', you first need to calculate the slope 'm' using the formula: m = (y2 - y1) / (x2 - x1). Then, substitute 'm' along with either point (x1, y1) or (x2, y2) into the equation y = mx + b to solve for 'b'.
-
Dealing with systems of equations: If you have a system of linear equations, you might need to use methods like substitution or elimination to solve for 'b' along with other variables.
-
Non-linear equations: The process described applies only to linear equations. If you're dealing with non-linear equations, different techniques will be required.
Troubleshooting Common Mistakes
Here are a few common mistakes to avoid when solving for 'b':
-
Incorrect order of operations: Remember to follow the order of operations (PEMDAS/BODMAS) accurately.
-
Errors in arithmetic: Double-check your calculations to minimize arithmetic errors.
-
Incorrect substitution: Ensure you substitute the given values correctly into the equation.
-
Forgetting to consider negative signs: Pay close attention to negative signs and ensure you handle them appropriately during the subtraction and addition steps.
Conclusion: Mastering the Art of Solving for b
Solving for 'b' in the equation y = mx + b is a fundamental algebraic skill with broad applications. By understanding the underlying principles and following the step-by-step process outlined above, you can confidently solve for 'b' in various scenarios, from simple arithmetic problems to more complex real-world applications. Remember to practice regularly and address any uncertainties to improve your proficiency. Mastering this skill will significantly enhance your understanding of linear equations and their use in various fields. Through consistent practice and attention to detail, you’ll confidently navigate the world of linear equations and unlock their power to solve real-world problems. The seemingly simple act of solving for 'b' opens doors to a deeper understanding of mathematics and its multifaceted applications.
Latest Posts
Latest Posts
-
How Many Degrees Is A Rectangle
Apr 05, 2025
-
How Do You Find The Lateral Area Of A Cone
Apr 05, 2025
-
What Is 4 6 As A Grade
Apr 05, 2025
-
What Are The Factors Of 61
Apr 05, 2025
-
What Is E To The Power Infinity
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Solving For B In Y Mx B . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
