What Are The Factors Of 93
News Co
Apr 05, 2025 · 6 min read
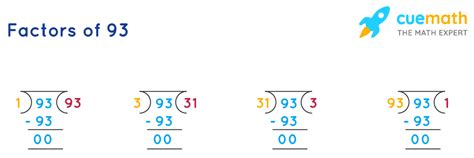
Table of Contents
What are the Factors of 93? A Deep Dive into Prime Factorization and Divisibility
Finding the factors of a number might seem like a simple mathematical task, but understanding the process reveals a deeper appreciation for number theory and its applications. This article explores the factors of 93, providing a comprehensive explanation of how to find them, why they're important, and the broader mathematical concepts involved. We'll go beyond a simple list, delving into prime factorization, divisibility rules, and the significance of these concepts in various fields.
Understanding Factors
Before we delve into the specifics of 93, let's define what factors are. A factor (or divisor) of a number is a whole number that divides that number exactly without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 evenly.
Finding the Factors of 93: A Step-by-Step Approach
There are several ways to find the factors of 93. The most straightforward approach is to systematically check each whole number, starting from 1, to see if it divides 93 without leaving a remainder. Let's do this:
-
Start with 1: 93 divided by 1 is 93, so 1 and 93 are factors.
-
Check 2: 93 is not divisible by 2 (it's not an even number).
-
Check 3: The divisibility rule for 3 states that a number is divisible by 3 if the sum of its digits is divisible by 3. 9 + 3 = 12, which is divisible by 3. Therefore, 3 is a factor. 93 divided by 3 is 31.
-
Check subsequent numbers: We continue checking numbers, but we can optimize our search. Since we found that 31 is a factor (93/3 = 31), we know that any factor larger than the square root of 93 (approximately 9.64) will have a corresponding factor smaller than the square root. Therefore, we only need to check numbers up to 9.
-
Numbers 4-9: 93 is not divisible by 4, 5, 6, 7, 8, or 9.
Therefore, the factors of 93 are 1, 3, 31, and 93.
Prime Factorization of 93
Prime factorization is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. The prime factorization of a number is unique.
We've already established that 3 and 31 are factors of 93. Both 3 and 31 are prime numbers. Therefore, the prime factorization of 93 is 3 x 31. This is a fundamental concept in number theory and has various applications in cryptography and other areas.
Divisibility Rules: Shortcuts to Finding Factors
Knowing divisibility rules can significantly speed up the process of finding factors. Here are some common rules:
-
Divisibility by 2: A number is divisible by 2 if it's even (ends in 0, 2, 4, 6, or 8).
-
Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
-
Divisibility by 4: A number is divisible by 4 if its last two digits are divisible by 4.
-
Divisibility by 5: A number is divisible by 5 if it ends in 0 or 5.
-
Divisibility by 6: A number is divisible by 6 if it's divisible by both 2 and 3.
-
Divisibility by 9: A number is divisible by 9 if the sum of its digits is divisible by 9.
-
Divisibility by 10: A number is divisible by 10 if it ends in 0.
These rules can be helpful in quickly eliminating numbers as potential factors.
Applications of Factors and Prime Factorization
The concept of factors and prime factorization isn't just a theoretical exercise. It has practical applications in many areas, including:
-
Cryptography: Prime numbers and prime factorization are fundamental to many modern encryption algorithms, ensuring secure online transactions and data protection. The difficulty of factoring very large numbers into their prime components forms the basis of the security of these systems.
-
Modular Arithmetic: Factors are crucial in modular arithmetic, which is used in various fields like computer science, cryptography, and clock arithmetic. Understanding divisibility helps in solving problems involving remainders and congruences.
-
Number Theory: Factors and prime factorization are core concepts in number theory, a branch of mathematics that deals with the properties and relationships of numbers. It has connections to other areas of mathematics, such as algebra and geometry.
-
Fractions and Simplifying Expressions: In algebra, understanding factors is essential for simplifying fractions and algebraic expressions. Finding the greatest common factor (GCF) of two numbers is crucial for reducing fractions to their simplest forms. This also helps in simplifying polynomials.
-
Data Structures and Algorithms: Efficient algorithms for finding factors and prime factorization are used in computer science for various tasks, including data analysis, optimization problems, and database management.
-
Scheduling and Resource Allocation: Divisibility plays a role in problems involving scheduling and resource allocation. For example, determining the optimal allocation of resources based on the factors involved in production processes.
Beyond the Basics: Exploring Advanced Concepts
The study of factors extends beyond the simple process of finding divisors. Here are some advanced concepts related to factors:
-
Greatest Common Factor (GCF): The greatest common factor of two or more numbers is the largest number that divides all of the numbers without leaving a remainder. For example, the GCF of 12 and 18 is 6.
-
Least Common Multiple (LCM): The least common multiple of two or more numbers is the smallest number that is a multiple of all the numbers. For example, the LCM of 4 and 6 is 12.
-
Perfect Numbers: A perfect number is a positive integer that is equal to the sum of its proper divisors (excluding itself). For example, 6 is a perfect number because its proper divisors (1, 2, and 3) add up to 6.
-
Abundant Numbers: An abundant number is a positive integer that is less than the sum of its proper divisors.
-
Deficient Numbers: A deficient number is a positive integer that is greater than the sum of its proper divisors.
Conclusion: The Significance of Understanding Factors
Understanding factors, prime factorization, and related concepts isn't just about mastering a mathematical skill; it's about gaining a deeper insight into the structure and behavior of numbers. This knowledge has far-reaching applications across numerous fields, highlighting the importance of this seemingly simple topic. From securing online transactions to simplifying algebraic expressions, the ability to analyze and manipulate factors is a valuable asset in various contexts. By exploring these concepts, we gain a more profound appreciation for the elegance and power of mathematics. The seemingly simple question, "What are the factors of 93?" leads us down a path of discovery that touches upon fundamental concepts with significant real-world implications.
Latest Posts
Latest Posts
-
What Is Prime Factorization Of 70
Apr 05, 2025
-
What Is A Factor Of 93
Apr 05, 2025
-
Find The Center And Radius Of The Circle
Apr 05, 2025
-
What Is A Fraction Equivalent To 2 3
Apr 05, 2025
-
Cuanto Es 45 Grados Fahrenheit En Centigrados
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors Of 93 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
