What Are The Prime Factors Of 625
News Co
Apr 05, 2025 · 5 min read
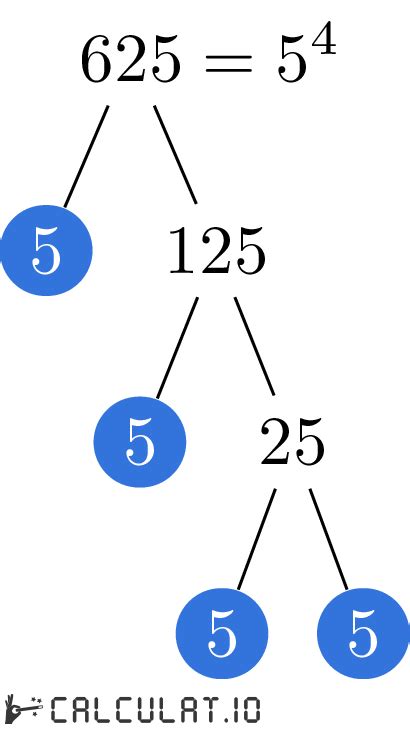
Table of Contents
What Are the Prime Factors of 625? A Deep Dive into Prime Factorization
Finding the prime factors of a number might seem like a simple mathematical exercise, but understanding the process reveals fundamental concepts in number theory and has practical applications in various fields, from cryptography to computer science. This article will explore the prime factorization of 625 in detail, explaining the methods involved and delving into the broader significance of prime numbers and prime factorization.
Understanding Prime Numbers and Prime Factorization
Before we delve into the specifics of 625, let's establish a solid foundation. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it's not divisible by any other whole number without leaving a remainder. The first few prime numbers are 2, 3, 5, 7, 11, and so on. They are the building blocks of all other whole numbers.
Prime factorization, also known as prime decomposition, is the process of breaking down a composite number (a number greater than 1 that is not prime) into its prime factors. Every composite number can be uniquely expressed as a product of prime numbers. This uniqueness is guaranteed by the Fundamental Theorem of Arithmetic. This theorem is a cornerstone of number theory, assuring us that the prime factorization of any number is unique (except for the order of the factors).
Methods for Finding Prime Factors
Several methods can be used to find the prime factors of a number. Let's explore a few common approaches, illustrating them with smaller numbers before tackling 625.
1. The Factor Tree Method
This is a visual method, particularly helpful for smaller numbers. You start by finding any two factors of the number. Then, you break down those factors further until you're left only with prime numbers.
Let's find the prime factors of 12 using the factor tree method:
- Start with 12. We can express it as 2 x 6.
- 2 is a prime number, but 6 is not. We break down 6 into 2 x 3.
- Both 2 and 3 are prime numbers.
Therefore, the prime factorization of 12 is 2 x 2 x 3, or 2² x 3.
2. Repeated Division by Prime Numbers
This method involves systematically dividing the number by the smallest prime numbers (2, 3, 5, 7, etc.) until you reach 1.
Let's find the prime factors of 30 using this method:
- 30 is divisible by 2: 30 ÷ 2 = 15
- 15 is divisible by 3: 15 ÷ 3 = 5
- 5 is a prime number.
Therefore, the prime factorization of 30 is 2 x 3 x 5.
3. Using the Sieve of Eratosthenes (for a range of numbers)
The Sieve of Eratosthenes is a powerful algorithm for finding all prime numbers up to a specified integer. While not directly a prime factorization method, it can be a helpful preliminary step, particularly if you need to factorize multiple numbers within a certain range. It works by iteratively marking as composite (non-prime) the multiples of each prime, starting with 2.
Finding the Prime Factors of 625
Now, let's apply these methods to find the prime factors of 625. The factor tree method might seem cumbersome for larger numbers, so we'll use the repeated division method.
- Check for divisibility by 2: 625 is not divisible by 2 (it's an odd number).
- Check for divisibility by 3: The sum of the digits (6 + 2 + 5 = 13) is not divisible by 3, so 625 is not divisible by 3.
- Check for divisibility by 5: 625 ends in 5, so it's divisible by 5. 625 ÷ 5 = 125
- Check for divisibility by 5 (again): 125 also ends in 5, so it's divisible by 5. 125 ÷ 5 = 25
- Check for divisibility by 5 (again): 25 ends in 5, so it's divisible by 5. 25 ÷ 5 = 5
- 5 is a prime number.
Therefore, the prime factorization of 625 is 5 x 5 x 5 x 5, or 5⁴.
The Significance of Prime Factorization
The seemingly simple act of prime factorization has far-reaching consequences in various fields:
1. Cryptography
Prime numbers play a crucial role in modern cryptography, particularly in public-key cryptography systems like RSA. The security of these systems relies on the difficulty of factoring very large numbers into their prime factors. The larger the numbers involved, the more computationally intensive the factorization becomes, making it practically impossible to break the encryption within a reasonable timeframe.
2. Number Theory
Prime factorization is a fundamental concept in number theory. Many theorems and concepts within number theory rely on the properties of prime numbers and their factorization. Understanding prime factorization helps us understand the structure and properties of whole numbers.
3. Computer Science
Algorithms for prime factorization are used in various computer science applications, including:
- Data Compression: Some compression algorithms use prime factorization to improve efficiency.
- Hashing: Prime numbers are often used in hash functions to minimize collisions and ensure data integrity.
- Random Number Generation: Prime numbers can be used in the design of pseudo-random number generators.
4. Other Applications
Prime factorization also finds applications in:
- Coding Theory: Error-correcting codes often utilize prime numbers.
- Physics: Prime numbers appear unexpectedly in various physical phenomena, although the reasons are not always fully understood.
Conclusion: Beyond the Numbers
Finding the prime factors of 625 – resulting in 5⁴ – might seem like a small mathematical problem, but it provides a window into the fascinating world of prime numbers and their profound impact on various fields. The seemingly simple process of prime factorization underlies many advanced mathematical concepts and practical applications, showcasing the power and beauty of fundamental mathematical principles. From the security of our online transactions to the development of advanced algorithms, prime numbers and their factorization continue to be essential tools in our technological world. Understanding these concepts allows for a deeper appreciation of the intricate workings of mathematics and its profound influence on our daily lives.
Latest Posts
Latest Posts
-
What Is The Percent Of 1 5
Apr 06, 2025
-
Convert 16 Degrees C To Fahrenheit
Apr 06, 2025
-
What Is A Constant Term In A Polynomial
Apr 06, 2025
-
What Is The Square Root Pi
Apr 06, 2025
-
Round Answer To 2 Decimal Places
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Are The Prime Factors Of 625 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
