What's The Prime Factorization Of 76
News Co
Apr 01, 2025 · 5 min read
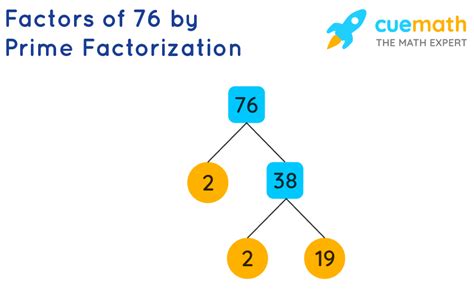
Table of Contents
What's the Prime Factorization of 76? A Deep Dive into Prime Numbers and Factorization
The seemingly simple question, "What's the prime factorization of 76?" opens a door to a fascinating world of number theory. While the answer itself is straightforward, exploring the process and the underlying concepts provides a rich understanding of prime numbers, factorization, and their significance in mathematics. This article will not only answer the question but delve into the theoretical foundations, practical applications, and even some related puzzles.
Understanding Prime Numbers
Before tackling the prime factorization of 76, let's solidify our understanding of prime numbers. A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This seemingly simple definition holds profound implications in mathematics. Prime numbers are the fundamental building blocks of all other natural numbers, much like atoms are the building blocks of matter.
Some examples of prime numbers include 2, 3, 5, 7, 11, 13, and so on. Notice that 2 is the only even prime number; all other even numbers are divisible by 2. The distribution of prime numbers is a subject of ongoing research, with mathematicians still exploring patterns and conjectures related to their distribution. The Prime Number Theorem, for instance, provides an approximation of the number of primes less than a given number.
Identifying Prime Numbers
Determining whether a given number is prime can be challenging for larger numbers. While simple divisibility tests exist for small numbers, more sophisticated algorithms are required for larger ones. The Sieve of Eratosthenes is a classic algorithm that efficiently identifies prime numbers up to a given limit. More advanced methods, such as probabilistic primality tests, are employed for extremely large numbers used in cryptography.
What is Prime Factorization?
Prime factorization is the process of expressing a composite number (a number greater than 1 that is not prime) as a product of its prime factors. Each composite number has a unique prime factorization, a fundamental theorem of arithmetic. This uniqueness is crucial in various mathematical applications.
For example, the prime factorization of 12 is 2 x 2 x 3, or 2² x 3. Notice that regardless of the order of the factors, the prime factorization remains the same. This unique decomposition is a cornerstone of many mathematical concepts.
Finding the Prime Factorization of 76
Now, let's address the initial question: what is the prime factorization of 76? We can approach this using a factor tree or by systematically dividing by prime numbers.
Method 1: Factor Tree
- Start by finding any two factors of 76. A simple observation reveals that 76 is an even number, so it's divisible by 2.
- 76 = 2 x 38
- Now, consider the factor 38. It's also an even number, divisible by 2.
- 38 = 2 x 19
- Finally, 19 is a prime number.
Therefore, the prime factorization of 76 is 2 x 2 x 19, or 2² x 19.
Method 2: Systematic Division
- Divide 76 by the smallest prime number, 2: 76 ÷ 2 = 38
- Divide 38 by 2: 38 ÷ 2 = 19
- 19 is a prime number.
Again, we arrive at the prime factorization: 2 x 2 x 19 or 2² x 19.
The Significance of Prime Factorization
The seemingly simple process of prime factorization has profound implications across various fields:
Cryptography
Prime factorization is the cornerstone of many modern cryptographic systems, including RSA encryption. The difficulty of factoring extremely large numbers into their prime factors forms the basis of the security of these systems. The larger the numbers, the more computationally intensive it becomes to find their prime factors, ensuring data security.
Number Theory
Prime factorization is a fundamental concept in number theory, used to prove various theorems and solve complex problems related to integers. Many unsolved problems in number theory, such as the Goldbach conjecture (every even integer greater than 2 can be expressed as the sum of two primes), rely on the properties of prime numbers and their factorization.
Computer Science
Algorithms related to prime factorization are crucial in computer science, particularly in areas like cryptography and data security. Efficient algorithms for prime factorization are constantly being developed and improved to meet the increasing demands of modern applications. The development of quantum computing poses a potential threat to RSA encryption because quantum computers could potentially factor large numbers much faster than classical computers.
Beyond 76: Exploring Other Factorizations
Let's examine a few more examples to further solidify our understanding:
- Prime Factorization of 100: 100 = 10 x 10 = 2 x 5 x 2 x 5 = 2² x 5²
- Prime Factorization of 252: 252 = 2 x 126 = 2 x 2 x 63 = 2 x 2 x 3 x 21 = 2 x 2 x 3 x 3 x 7 = 2² x 3² x 7
- Prime Factorization of 1000: 1000 = 10 x 10 x 10 = (2 x 5) x (2 x 5) x (2 x 5) = 2³ x 5³
These examples demonstrate the consistent application of the process, regardless of the size or complexity of the number.
Practical Applications and Puzzles
Prime factorization extends beyond theoretical mathematics and finds practical applications in everyday life, though often indirectly. Here are a couple of examples:
Divisibility Rules
Understanding prime factorization aids in understanding divisibility rules. For instance, a number is divisible by 4 if its last two digits form a number divisible by 4. This stems from the prime factorization of 4 (2²). Similarly, divisibility rules for other numbers are related to their prime factorizations.
Puzzles and Games
Prime factorization can form the basis of intriguing mathematical puzzles and games. For example, puzzles might involve finding a number with specific prime factors or determining the smallest number with a given set of prime factors. These puzzles can be a fun and engaging way to reinforce the concepts of prime numbers and factorization.
Conclusion
The prime factorization of 76, 2² x 19, is more than just a simple calculation. It's a gateway to understanding the fundamental building blocks of numbers and their profound implications in mathematics, computer science, and cryptography. Exploring prime factorization not only enhances mathematical skills but also cultivates a deeper appreciation for the elegance and power of number theory. The seemingly simple question, "What's the prime factorization of 76?" unveils a world of intricate connections and far-reaching applications. Further exploration into the fascinating world of prime numbers promises even more exciting discoveries and challenges.
Latest Posts
Latest Posts
-
How To Convert A Ratio To A Percentage
Apr 02, 2025
-
Least Common Multiple Of 6 8 And 15
Apr 02, 2025
-
What Factors Do 18 And 30 Have In Common
Apr 02, 2025
-
How Many Minutes Is 120 Seconds
Apr 02, 2025
-
Lcm For 3 4 And 5
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What's The Prime Factorization Of 76 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
