X Less Than Or Equal To 2
News Co
May 08, 2025 · 5 min read
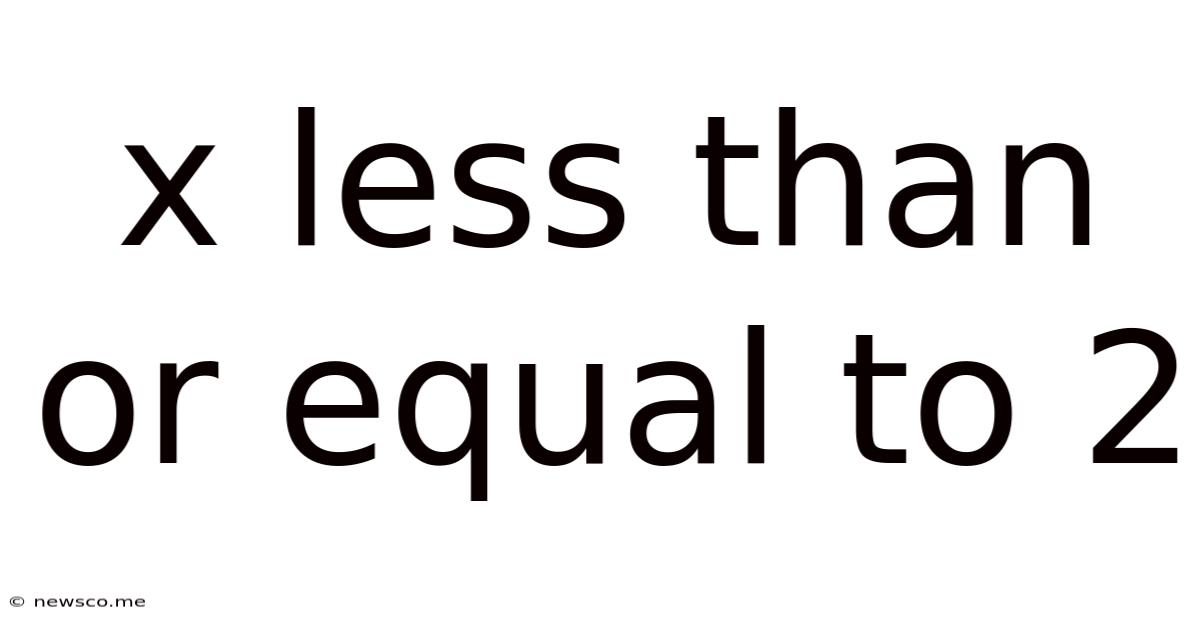
Table of Contents
x ≤ 2: A Comprehensive Exploration of Inequalities
Inequalities are fundamental concepts in mathematics, forming the bedrock for problem-solving in various fields, from basic algebra to advanced calculus and beyond. Understanding inequalities is crucial for grasping concepts like limits, ranges, and domains, all essential for a robust understanding of mathematical modeling and real-world applications. This article delves into the inequality x ≤ 2, exploring its meaning, graphical representation, applications, and extensions to more complex scenarios.
Understanding the Inequality x ≤ 2
The inequality x ≤ 2 is read as "x is less than or equal to 2". This simple statement encapsulates a powerful idea: the variable x can represent any value that is either less than 2 or equal to 2. This contrasts with an equation, like x = 2, which only has one solution. The inequality x ≤ 2 has an infinite number of solutions.
Key Components:
- x: This represents an unknown variable, which could be any real number.
- ≤: This symbol denotes "less than or equal to". This crucial element signifies that x can be 2, or any value smaller than 2.
- 2: This is a constant, representing the upper bound of the possible values of x.
Visualizing the Inequality: The Number Line
The most straightforward way to visualize x ≤ 2 is using a number line. A number line is a horizontal line where numbers are placed according to their value, with smaller numbers to the left and larger numbers to the right.
To represent x ≤ 2 on a number line:
- Locate 2: Find the point representing the number 2 on the number line.
- Draw a Closed Circle: Place a closed circle (or a filled-in circle) on the number 2. This indicates that 2 is included in the solution set.
- Shade to the Left: Shade the number line to the left of 2. This represents all the numbers less than 2.
The shaded region, along with the closed circle at 2, visually represents all the values of x that satisfy the inequality x ≤ 2.
Solving Inequalities Involving x ≤ 2
While x ≤ 2 is a simple inequality, it can be part of more complex problems. Understanding how to manipulate inequalities is essential for solving these problems. The fundamental rule is: you can perform the same operation (addition, subtraction, multiplication, or division) on both sides of the inequality, as long as you don't multiply or divide by a negative number. If you do multiply or divide by a negative number, you must reverse the inequality sign.
Example 1: Solving a Simple Inequality
Let's consider the inequality: x + 3 ≤ 5. To solve for x, we subtract 3 from both sides:
x + 3 - 3 ≤ 5 - 3
x ≤ 2
This shows that the solution to x + 3 ≤ 5 is the same as the solution to x ≤ 2.
Example 2: Inequality with Multiplication
Solve the inequality: 2x ≤ 4. To isolate x, we divide both sides by 2:
2x / 2 ≤ 4 / 2
x ≤ 2
Again, the solution is x ≤ 2.
Example 3: Inequality with Negative Multiplication
Solve the inequality: -2x ≤ 4. To isolate x, we divide both sides by -2. Remember to reverse the inequality sign!
-2x / -2 ≥ 4 / -2
x ≥ -2
Notice how the inequality sign flipped from ≤ to ≥.
Applications of x ≤ 2 and Related Inequalities
The inequality x ≤ 2 and its variations find applications in numerous fields:
1. Real-World Scenarios:
- Manufacturing: A machine can only produce a maximum of 2 units per hour. The number of units produced (x) must be less than or equal to 2 (x ≤ 2).
- Budgeting: You have a budget of $2. The cost of an item (x) must be less than or equal to your budget (x ≤ 2).
- Temperature: The temperature must remain at or below 2 degrees Celsius (x ≤ 2°C).
2. Interval Notation:
Inequalities can be represented using interval notation. For x ≤ 2, the interval notation is (-∞, 2], where:
- (-∞): Represents negative infinity, indicating that there's no lower limit.
- 2]: Represents the upper limit, 2, which is included (hence the square bracket).
3. Set Theory:
The solution to x ≤ 2 can be represented as a set: {x | x ∈ ℝ, x ≤ 2}. This reads as "the set of all x such that x is a real number and x is less than or equal to 2".
4. Graphing Functions:
Inequalities are crucial for defining the domain and range of functions. For example, if a function is defined only for x ≤ 2, this restricts the input values to those satisfying the inequality.
5. Linear Programming:
Linear programming problems, used extensively in optimization, involve inequalities like x ≤ 2 to define constraints on the variables.
Extending the Concept: Compound Inequalities
The inequality x ≤ 2 can be combined with other inequalities to create compound inequalities. These involve multiple inequalities that must be satisfied simultaneously.
Example: Compound Inequality
Consider the compound inequality: 1 ≤ x ≤ 2. This means x must be greater than or equal to 1 and less than or equal to 2. It represents a closed interval [1, 2] on the number line.
Solving Compound Inequalities:
Solving compound inequalities requires solving each inequality separately and then finding the intersection of the solution sets.
Advanced Applications: Calculus and Beyond
Inequalities are fundamental in calculus, particularly when dealing with limits and derivatives. Understanding inequalities allows one to determine the behavior of functions as x approaches certain values. In real analysis, inequalities play a pivotal role in establishing convergence and divergence of sequences and series.
For instance, inequalities help establish bounds on the error in approximations or determine the convergence radius of power series. They are essential tools for proving important theorems and solving complex problems in advanced mathematics and its applications in physics, engineering, and computer science.
Conclusion: The Significance of x ≤ 2
The simple inequality x ≤ 2 might seem elementary, but it's a building block for a vast array of mathematical concepts and applications. From basic algebra to advanced calculus and real-world problem-solving, understanding and manipulating inequalities is crucial for anyone pursuing a deeper understanding of mathematics and its power to model and solve problems in the real world. This comprehensive exploration illustrates the multifaceted nature of this seemingly simple inequality and its essential role in the broader landscape of mathematics. The ability to visualize, solve, and apply inequalities such as x ≤ 2 is a fundamental skill with far-reaching implications in various fields of study and professional practice.
Latest Posts
Latest Posts
-
What Ratio Is Equivalent To 5 4
May 08, 2025
-
20 Percent Of What Number Is 10
May 08, 2025
-
Which Of The Following Expressions Is Written In Scientific Notation
May 08, 2025
-
What Is The Area Of The Following Figure
May 08, 2025
-
How Many Parallel Lines Does A Pentagon Have
May 08, 2025
Related Post
Thank you for visiting our website which covers about X Less Than Or Equal To 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.