Lcm Of 2 3 And 6
News Co
Apr 05, 2025 · 5 min read
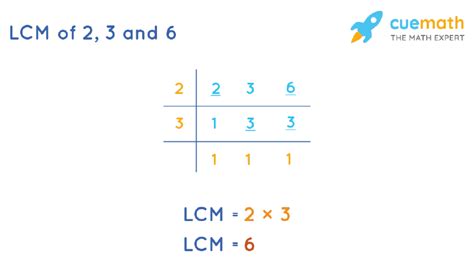
Table of Contents
Understanding the LCM of 2, 3, and 6: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex equations. This article delves deep into understanding the LCM of 2, 3, and 6, explaining the process in detail, exploring different methods, and showcasing its practical significance. We'll also touch upon the broader context of LCM calculations and its role in more advanced mathematical concepts.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's the smallest number that contains all the numbers in the set as factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3.
Understanding the concept of divisibility is key. A number is divisible by another number if the division results in a whole number (no remainder). Therefore, when we seek the LCM, we’re looking for the smallest number that can be cleanly divided by all the given numbers.
Calculating the LCM of 2, 3, and 6: Three Proven Methods
Let’s now focus on calculating the LCM of 2, 3, and 6. We'll explore three common and effective methods:
Method 1: Listing Multiples
This is a straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16…
- Multiples of 3: 3, 6, 9, 12, 15, 18…
- Multiples of 6: 6, 12, 18, 24…
By examining the lists, we can easily see that the smallest multiple common to all three numbers is 6.
Method 2: Prime Factorization
This method is more efficient for larger numbers or a greater number of integers. It involves finding the prime factorization of each number and then constructing the LCM from the prime factors.
- Prime factorization of 2: 2
- Prime factorization of 3: 3
- Prime factorization of 6: 2 x 3
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
Therefore, the LCM of 2, 3, and 6 is 2 x 3 = 6.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b) = (a x b) / GCD(a, b)
This formula can be extended to more than two numbers. However, for the sake of simplicity, let's apply it pairwise. First, let's find the LCM of 2 and 3:
- GCD(2, 3) = 1 (since 2 and 3 share no common factors other than 1)
- LCM(2, 3) = (2 x 3) / 1 = 6
Now, let's find the LCM of this result (6) and the remaining number (6):
- GCD(6, 6) = 6
- LCM(6, 6) = (6 x 6) / 6 = 6
Therefore, the LCM of 2, 3, and 6 is 6.
Why is Understanding LCM Important?
The LCM isn't just an abstract mathematical concept; it has numerous practical applications:
1. Fraction Operations
Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For example, to add 1/2 and 1/3, we find the LCM of 2 and 3 (which is 6), and then rewrite the fractions with a denominator of 6 before adding them.
2. Scheduling and Timing Problems
LCM is useful in solving problems involving cyclical events. For instance, if two machines operate on different cycles (say, one every 2 hours and the other every 3 hours), finding the LCM (6 hours) tells us when both machines will operate simultaneously again.
3. Pattern Recognition and Sequences
Identifying repeating patterns or cycles in sequences often involves finding the LCM. This is particularly relevant in fields like music theory, where understanding rhythmic patterns depends on identifying common multiples.
4. Number Theory and Cryptography
LCM plays a significant role in number theory, which forms the foundation of modern cryptography. Many cryptographic algorithms rely on properties of LCM and related concepts.
5. Real-World Applications
From coordinating schedules for construction projects to calculating when celestial bodies align, LCM finds practical applications across diverse fields.
Expanding on LCM Concepts: Beyond the Basics
While we've focused on the LCM of 2, 3, and 6, understanding the broader context of LCM calculations is crucial.
Calculating LCM for Larger Sets of Numbers
The methods described earlier—prime factorization and the GCD approach—are particularly effective when dealing with more than three numbers or larger numbers. The prime factorization method remains generally efficient, especially for numbers with many factors. For larger sets of numbers, specialized algorithms may improve computational efficiency.
Relationship Between LCM and GCD
The relationship between LCM and GCD is fundamental in number theory. The formula LCM(a, b) x GCD(a, b) = a x b is a powerful tool for efficiently calculating either the LCM or GCD if the other is known. This relationship simplifies calculations, especially when dealing with large numbers.
LCM in Abstract Algebra
The concept of LCM extends beyond integers to other mathematical structures in abstract algebra. The generalization of LCM finds applications in more advanced mathematical areas.
Conclusion: The Importance of Mastering LCM
Mastering the concept of LCM is essential for anyone pursuing a deeper understanding of mathematics. From simplifying fractions to solving complex scheduling problems, the ability to calculate the LCM quickly and accurately is a valuable skill. The methods discussed—listing multiples, prime factorization, and using the GCD—provide versatile tools for tackling LCM calculations in various contexts. Understanding the relationship between LCM and GCD further enhances one's mathematical toolkit, paving the way for exploration of more advanced mathematical concepts. The LCM of 2, 3, and 6, though seemingly simple, serves as a solid foundation for comprehending this crucial mathematical concept and its widespread applications.
Latest Posts
Latest Posts
-
What Fractions Are Equal To 1 4
Apr 05, 2025
-
Formula Of Perimeter Of Regular Polygon
Apr 05, 2025
-
What Are The Prime Factors Of 625
Apr 05, 2025
-
What Is 4 To The 2 Power
Apr 05, 2025
-
What Is 5 To The Fifth Power
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 2 3 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
