What Is E To The Power Infinity
News Co
Apr 05, 2025 · 5 min read
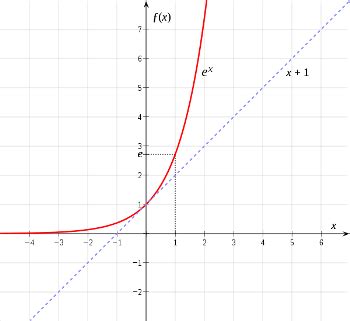
Table of Contents
What is e to the Power of Infinity? Unraveling the Mysteries of Exponential Growth
The expression "e to the power of infinity," often written as e<sup>∞</sup>, is a fascinating and conceptually challenging topic in mathematics. It's not a straightforward calculation like 2<sup>3</sup> = 8, but rather a limit, representing the behavior of e<sup>x</sup> as x grows without bound. Understanding this requires delving into the nature of exponential functions, limits, and the unique properties of Euler's number, e. This exploration will demystify this seemingly paradoxical expression and illuminate its significance in various fields.
Understanding Exponential Growth and the Number e
Before tackling e<sup>∞</sup>, it's crucial to grasp the concept of exponential growth and the significance of e. Exponential growth describes a phenomenon where a quantity increases at a rate proportional to its current value. Imagine a bacterial colony doubling in size every hour. The growth isn't linear; it accelerates dramatically over time. This type of growth is modeled using exponential functions of the form:
f(x) = a<sup>x</sup>
where 'a' is the base and 'x' is the exponent. Different bases lead to different growth rates. The number e, approximately 2.71828, holds a special place in mathematics because its exponential function, e<sup>x</sup>, possesses unique properties. Specifically, its derivative is equal to itself (d/dx e<sup>x</sup> = e<sup>x</sup>), a characteristic that simplifies numerous calculations in calculus and differential equations. This self-similarity makes e the natural base for exponential functions, hence the term "natural exponential function" for e<sup>x</sup>.
The Significance of the Natural Exponential Function
The prevalence of e in nature underscores its importance. It appears in diverse contexts, from radioactive decay and compound interest to the normal distribution in statistics and the shape of a hanging chain (catenary). Its self-replicating property within calculus makes it particularly useful in modeling continuous growth and decay processes. This ubiquitous nature is why understanding its behavior as the exponent approaches infinity is essential.
Exploring the Limit: e<sup>∞</sup>
The expression e<sup>∞</sup> is not a definitive value but rather represents the limit of the function e<sup>x</sup> as x approaches infinity:
lim<sub>x→∞</sub> e<sup>x</sup> = ∞
This means that as x gets arbitrarily large, the value of e<sup>x</sup> grows without bound. There's no finite number that e<sup>x</sup> approaches; it increases indefinitely. This is a direct consequence of the exponential nature of the function. Each increment in x multiplies the previous value by e, leading to ever-increasing magnitudes.
Visualizing the Limit
Consider plotting the graph of y = e<sup>x</sup>. As you move along the x-axis towards positive infinity, the y-values climb relentlessly upwards, never plateauing or approaching a horizontal asymptote. This visual representation reinforces the concept that e<sup>∞</sup> represents unbounded growth, not a specific numerical value.
Differentiating e<sup>∞</sup> from other limits
It's important to distinguish the behavior of e<sup>∞</sup> from other limits involving infinity. For instance:
- lim<sub>x→∞</sub> 1/x = 0: The reciprocal function approaches zero as x grows without bound.
- lim<sub>x→∞</sub> sin(x): This limit does not exist, as the sine function oscillates between -1 and 1, never settling on a specific value.
In contrast, e<sup>x</sup> consistently increases, unequivocally tending towards infinity.
Applications of e<sup>∞</sup> and Unbounded Growth
While e<sup>∞</sup> doesn't represent a specific number, the concept of unbounded exponential growth it embodies has far-reaching applications:
1. Modeling Uncontrolled Growth:
Numerous real-world scenarios exhibit exponential growth, at least initially. These include:
- Population growth: Under ideal conditions, a population's growth can be modeled using an exponential function. However, resource limitations and other factors ultimately limit growth.
- Spread of infectious diseases: In the early stages of an epidemic, the number of infected individuals can increase exponentially before interventions or natural immunity slow the spread.
- Financial investments: Compound interest, if left untouched, results in exponential growth of the principal amount. The longer the investment period, the more pronounced this effect becomes.
2. Understanding Divergent Series:
In calculus, infinite series play a critical role. Some series converge to a finite sum, while others diverge, meaning their sum grows without bound. The behavior of e<sup>x</sup> as x approaches infinity helps determine the convergence or divergence of certain series. For example, understanding the limit of e<sup>x</sup> as x approaches infinity is often crucial for determining the radius of convergence of power series.
3. Probability and Statistics:
The normal distribution, a cornerstone of statistics, uses the exponential function in its formulation. While the probability of observing an extremely large value in a normal distribution is incredibly small, it's not zero. The tails of the distribution extend infinitely in both directions, reflecting the unbounded nature of the exponential function.
Beyond the Limit: Considerations for Practical Applications
While the mathematical concept of e<sup>∞</sup> signifies unbounded growth, real-world applications rarely encounter truly infinite growth. Factors like resource constraints, environmental limitations, and regulatory interventions typically impose limits on exponential growth. Therefore, in practical applications, models incorporating exponential growth often incorporate mechanisms to account for these constraints, leading to more realistic representations of real-world phenomena. These models might include logistic growth functions or other variations that incorporate limiting factors.
Conclusion: A Powerful Concept with Real-World Implications
The expression e<sup>∞</sup>, while not a numerical result, embodies the powerful concept of unbounded exponential growth. This concept, far from being a purely theoretical construct, finds practical application in diverse fields, helping us to model and understand phenomena ranging from population dynamics and the spread of disease to financial investments and statistical distributions. By appreciating the significance of e and understanding the behavior of its exponential function as the exponent approaches infinity, we gain valuable tools for analyzing and predicting complex systems. The seemingly simple expression e<sup>∞</sup> opens a window into a world of continuous, accelerating change, a world that is constantly shaped by the relentless power of exponential growth.
Latest Posts
Latest Posts
-
What Is 5 To The Fifth Power
Apr 05, 2025
-
What Is The Lcm Of 3 5
Apr 05, 2025
-
How To Find Height Of Parallelogram
Apr 05, 2025
-
What Is The Factor Of 31
Apr 05, 2025
-
How Many Sides Does An Octagon
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is E To The Power Infinity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
