What Are The Factors Of 92
News Co
Apr 05, 2025 · 5 min read
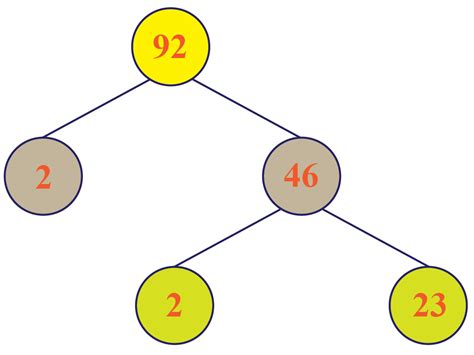
Table of Contents
Unveiling the Factors of 92: A Deep Dive into Number Theory
The seemingly simple question, "What are the factors of 92?" opens a door to a fascinating world of number theory. While the immediate answer might seem straightforward, exploring this question allows us to delve into fundamental concepts like prime factorization, divisibility rules, and the properties of even and odd numbers. This comprehensive exploration will not only provide the factors of 92 but also build a solid understanding of the underlying mathematical principles.
Understanding Factors and Divisibility
Before we tackle the factors of 92, let's define what a factor is. A factor (or divisor) of a number is a whole number that divides the number exactly, leaving no remainder. In simpler terms, if you can divide a number by another number without getting a fraction or decimal, the second number is a factor of the first. Divisibility is the key concept here; it refers to the ability of one number to be divided evenly by another.
Finding the Factors of 92: A Step-by-Step Approach
The most straightforward way to find the factors of 92 is to systematically check each whole number from 1 up to 92. However, this method can be tedious, especially with larger numbers. A more efficient approach involves utilizing our knowledge of divisibility rules and prime factorization.
Let's begin by checking the smallest factors:
- 1: Every number is divisible by 1, so 1 is a factor of 92.
- 2: 92 is an even number, meaning it's divisible by 2. 92 ÷ 2 = 46. Therefore, 2 is a factor.
- 4: Since 92 is divisible by 2, let's check if it's divisible by 4. 92 ÷ 4 = 23. Thus, 4 is a factor.
Now, we've identified 1, 2, and 4 as factors. Notice that 23 is also a factor (from the division by 4). This suggests that we've found a pair of factors that multiply to 92 (4 x 23 = 92).
Let's continue our search:
- 23: We've already established 23 as a factor.
- 46: We know that 92 ÷ 2 = 46, so 46 is a factor.
We've now found four factors: 1, 2, 4, and 23, 46. As we continue checking, we'll realize that the remaining factors are just the reverse pairs of the ones we already discovered. This is because factors come in pairs. When you find a factor x, you automatically find another factor, y, where x * y = 92.
Therefore, the complete set of factors for 92 is: 1, 2, 4, 23, 46, and 92.
Prime Factorization: A Powerful Tool
Prime factorization is a fundamental concept in number theory that involves expressing a number as a product of its prime factors. Prime numbers are whole numbers greater than 1 that have only two factors: 1 and themselves (e.g., 2, 3, 5, 7, 11). Prime factorization provides a systematic and efficient way to find all the factors of a number.
Let's find the prime factorization of 92:
- We know 92 is an even number, so it's divisible by 2: 92 = 2 x 46.
- 46 is also even, so it's divisible by 2: 46 = 2 x 23.
- 23 is a prime number.
Therefore, the prime factorization of 92 is 2 x 2 x 23, or 2² x 23.
Connecting Prime Factorization to All Factors
Understanding the prime factorization helps us systematically find all the factors of 92. We can generate factors by combining the prime factors in different ways:
- Using only the prime factors: 2, 23
- Combining prime factors: 2 x 2 = 4, 2 x 23 = 46, 2 x 2 x 23 = 92
- Including 1: 1
This method confirms our earlier list of factors: 1, 2, 4, 23, 46, and 92.
Exploring the Properties of Factors: Even and Odd Numbers
Observing the factors of 92 reveals an interesting pattern concerning even and odd numbers. Since 92 is an even number, it's not surprising that many of its factors are also even (2, 4, 46, 92). However, it also has one odd factor: 23. This illustrates that even numbers can have both even and odd factors. The presence of the odd factor 23 is a direct consequence of the prime factorization which includes the odd prime number 23.
Divisibility Rules: Shortcuts to Factor Finding
Knowing divisibility rules can significantly speed up the process of finding factors. Some useful rules include:
- Divisibility by 2: A number is divisible by 2 if it's even (ends in 0, 2, 4, 6, or 8).
- Divisibility by 3: A number is divisible by 3 if the sum of its digits is divisible by 3.
- Divisibility by 4: A number is divisible by 4 if its last two digits are divisible by 4.
- Divisibility by 5: A number is divisible by 5 if it ends in 0 or 5.
- Divisibility by 10: A number is divisible by 10 if it ends in 0.
By applying these rules, we can quickly determine some of the factors of a number without performing lengthy divisions.
Applications of Factors: Beyond the Basics
Understanding factors extends far beyond simple number theory. Factors play a crucial role in various mathematical concepts and real-world applications:
- Simplifying Fractions: Finding the greatest common factor (GCF) of the numerator and denominator allows us to simplify fractions to their lowest terms.
- Solving Equations: Factoring polynomials is essential in solving algebraic equations.
- Geometry: Factors are involved in calculating areas and volumes of geometric shapes.
- Computer Science: Factorization is a cornerstone of cryptography, particularly in public-key encryption algorithms.
Conclusion: The Richness of Factorization
The seemingly simple task of finding the factors of 92 has led us on a journey through fundamental number theory concepts. We've learned about prime factorization, divisibility rules, and the properties of even and odd numbers. This exploration highlights the importance of understanding these concepts, not only for solving mathematical problems but also for appreciating the underlying structure and beauty of numbers. The factors of 92—1, 2, 4, 23, 46, and 92—represent more than just a list; they represent a glimpse into the fascinating world of mathematics and its wide-ranging applications. Through a deeper understanding of factors, we unlock a more profound appreciation of the elegance and intricacy of numbers. The seemingly simple question of what are the factors of 92 is, therefore, much more than a simple query; it is a gateway to a vast mathematical landscape.
Latest Posts
Latest Posts
-
What Is The Prime Number Of 50
Apr 05, 2025
-
What Is The Square Root Of 149
Apr 05, 2025
-
What Is The Squar Root Of 81
Apr 05, 2025
-
How To Find The Zeros Of A Cubic Function
Apr 05, 2025
-
What Is 6 Percent Of 8
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Are The Factors Of 92 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
