What Is The Prime Number Of 50
News Co
Apr 05, 2025 · 6 min read
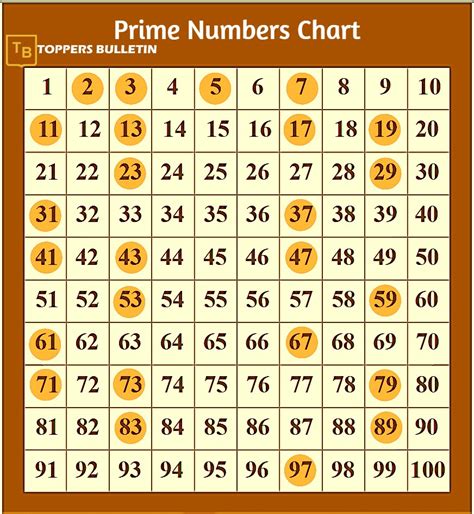
Table of Contents
What is the Prime Number of 50? Unveiling the Mysteries of Prime Numbers and the Sieve of Eratosthenes
The question "What is the prime number of 50?" might seem simple at first glance. However, it touches upon a fundamental concept in mathematics: prime numbers. Understanding what constitutes a prime number and how to identify them, particularly within a given range, requires exploring both the definition of prime numbers and efficient methods for finding them. This article delves into these aspects, explaining not only the answer to the initial question but also the broader context of prime number theory and its applications.
Understanding Prime Numbers: The Building Blocks of Arithmetic
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. In simpler terms, a prime number is only divisible without a remainder by 1 and itself. For example, 2, 3, 5, 7, and 11 are prime numbers. The number 4, however, is not prime because it's divisible by 2. Similarly, 9 is not prime because it's divisible by 3.
The importance of prime numbers stems from their fundamental role in number theory. They are the building blocks of all other natural numbers through a process called prime factorization. Every composite number (a number that is not prime) can be expressed as a unique product of prime numbers. This is known as the Fundamental Theorem of Arithmetic. For instance, the number 12 can be factored as 2 x 2 x 3 (or 2² x 3). This unique factorization is crucial in various mathematical fields and has practical applications in cryptography and computer science.
Identifying Prime Numbers: Methods and Algorithms
Determining whether a given number is prime can be straightforward for smaller numbers, but it becomes increasingly complex as numbers grow larger. Several methods exist to identify prime numbers, ranging from simple trial division to sophisticated algorithms.
Trial Division: A Simple Approach
The most basic method is trial division. This involves testing whether a number is divisible by any integer from 2 up to its square root. If it's not divisible by any of these numbers, it's prime. While simple to understand, trial division becomes computationally expensive for very large numbers.
The Sieve of Eratosthenes: An Efficient Algorithm
A more efficient algorithm for finding prime numbers is the Sieve of Eratosthenes. This ancient algorithm works by iteratively marking composite numbers as non-prime. It starts by listing all natural numbers up to a specified limit. Then, it repeatedly marks multiples of each prime number, starting with 2, as non-prime. The numbers that remain unmarked are prime. The Sieve of Eratosthenes offers a significantly faster way to generate a list of prime numbers compared to individual trial divisions, especially for larger ranges.
Finding the 50th Prime Number: Applying the Sieve
To answer the original question – what is the 50th prime number? – we can apply the Sieve of Eratosthenes or a similar algorithm. We need to generate a list of prime numbers until we reach the 50th number in the sequence.
Let's illustrate this process:
- Start with the number 2: This is the first prime number.
- Mark all multiples of 2 as non-prime: 4, 6, 8, 10, and so on.
- Move to the next unmarked number, which is 3: This is the second prime number.
- Mark all multiples of 3 as non-prime: 6 (already marked), 9, 12 (already marked), 15, and so on.
- Continue this process with the next unmarked numbers: 5, 7, 11, 13, and so on. Each unmarked number represents a prime number.
Continuing this process, you'll eventually arrive at the 50th prime number. It's important to note that this process becomes tedious manually for larger prime numbers. Computational tools or programming languages are often used to perform this task efficiently for larger numbers.
The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97...
By continuing this sequence, we can identify the 50th prime number, which is 229.
The Distribution of Prime Numbers: Exploring Patterns and Conjectures
The distribution of prime numbers across the number line is a fascinating and complex topic that has captivated mathematicians for centuries. While primes appear randomly at first glance, there are underlying patterns and relationships that are still being researched today.
The Prime Number Theorem: An Approximation
The Prime Number Theorem provides an approximation of the number of primes less than a given number. It states that the number of primes less than x is approximately x / ln(x), where ln(x) is the natural logarithm of x. This theorem doesn't give an exact count, but it provides a useful estimate for large values of x.
Twin Primes and Other Conjectures: Ongoing Research
The study of prime numbers also involves exploring specific types of primes and their distributions. Twin primes, which are pairs of prime numbers that differ by 2 (e.g., 3 and 5, 11 and 13), are a particularly interesting area of research. The Twin Prime Conjecture suggests that there are infinitely many twin prime pairs. This remains unproven, highlighting the ongoing mysteries surrounding the distribution of prime numbers. Other conjectures and unsolved problems related to prime numbers continue to drive research in number theory.
Applications of Prime Numbers: From Cryptography to Computer Science
Prime numbers, despite their seemingly abstract nature, have significant practical applications in various fields.
Cryptography: Securing Online Communications
Prime numbers are the cornerstone of many modern cryptographic systems. Algorithms like RSA encryption, widely used to secure online transactions and communications, rely heavily on the difficulty of factoring large numbers into their prime components. The complexity of this factorization forms the basis of the security of these systems.
Hashing Algorithms: Data Integrity and Security
Prime numbers also play a role in hashing algorithms, which are used to ensure the integrity and security of data. Hashing functions use prime numbers to help distribute data evenly across a hash table, improving efficiency and reducing collisions.
Computer Science: Algorithms and Data Structures
Prime numbers find applications in various algorithms and data structures in computer science. Their unique properties are exploited to optimize performance and efficiency in specific tasks.
Conclusion: The Enduring Significance of Prime Numbers
The question "What is the prime number of 50?" serves as a gateway to exploring the fascinating world of prime numbers. From their fundamental role in arithmetic to their crucial applications in cryptography and computer science, prime numbers continue to fascinate and challenge mathematicians and computer scientists alike. Understanding prime numbers, their properties, and their distribution is essential not only for appreciating the beauty of mathematics but also for comprehending the underlying principles of many technological advancements that shape our modern world. The search for patterns, the solving of conjectures, and the constant discovery of new properties related to prime numbers continue to be active areas of research, ensuring that the study of these fundamental building blocks will remain relevant and engaging for generations to come. The seemingly simple question of finding the 50th prime number opens a door to a vast and intricate field, highlighting the enduring significance and enduring mysteries surrounding these fundamental numbers.
Latest Posts
Latest Posts
-
What Is One Third Of 12
Apr 06, 2025
-
How Many Symmetrical Lines Does A Rectangle Have
Apr 06, 2025
-
What Is 1 To The 3rd Power
Apr 06, 2025
-
How Do You Find The Diagonal Of A Parallelogram
Apr 06, 2025
-
Figure Abcd Is A Parallelogram What Is The Value Of X
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Number Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
