What Is 2 Divided By 1 3
News Co
Apr 05, 2025 · 5 min read
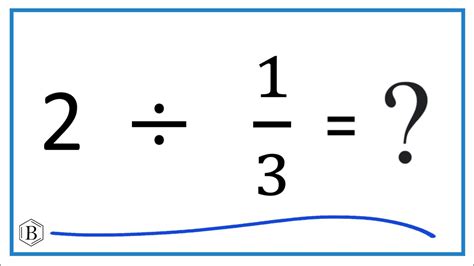
Table of Contents
- What Is 2 Divided By 1 3
- Table of Contents
- What is 2 Divided by 1/3? Understanding Fractions and Division
- Understanding Fraction Division: The "Keep, Change, Flip" Method
- Visualizing the Division: The "How Many Times?" Approach
- Reciprocal Understanding: The Core of Fraction Division
- Working with Mixed Numbers: A Step-by-Step Guide
- Real-World Applications: Putting It All Together
- Troubleshooting Common Mistakes
- Advanced Concepts: Extending Your Knowledge
- Conclusion: Mastering Fraction Division
- Latest Posts
- Latest Posts
- Related Post
What is 2 Divided by 1/3? Understanding Fractions and Division
The question "What is 2 divided by 1/3?" might seem deceptively simple at first glance. However, it provides a fantastic opportunity to delve into the fundamentals of fraction division, a concept often misunderstood by many. This comprehensive guide will not only answer the question but also explain the underlying principles, providing you with the tools to tackle similar problems with confidence. We'll explore various methods, explain the reasoning behind each step, and touch upon real-world applications to solidify your understanding.
Understanding Fraction Division: The "Keep, Change, Flip" Method
The most common method for dividing fractions involves a technique often remembered by the mnemonic "Keep, Change, Flip" (or KCF). Let's break down what this means:
-
Keep: Keep the first fraction (the dividend) exactly as it is. In our case, this is the number 2, which we can represent as the fraction 2/1.
-
Change: Change the division sign to a multiplication sign.
-
Flip: Flip the second fraction (the divisor) – this means inverting the numerator and denominator. Our divisor is 1/3, so flipping it gives us 3/1.
Applying the KCF method to our problem, we get:
2/1 ÷ 1/3 becomes 2/1 × 3/1
Now, we simply multiply the numerators together and the denominators together:
(2 × 3) / (1 × 1) = 6/1 = 6
Therefore, 2 divided by 1/3 equals 6.
Visualizing the Division: The "How Many Times?" Approach
Another way to understand fraction division is to think about it in terms of "how many times does the divisor fit into the dividend?"
Imagine you have 2 pizzas, and each serving is 1/3 of a pizza. How many servings can you get from the 2 pizzas?
To solve this visually, you can imagine dividing each pizza into three equal slices. Each pizza will yield 3 servings (3 slices). Since you have 2 pizzas, you'll have a total of 2 x 3 = 6 servings. This visualization reinforces the answer we obtained using the KCF method.
Reciprocal Understanding: The Core of Fraction Division
The "Flip" part of the KCF method involves finding the reciprocal of the divisor. The reciprocal of a number is simply 1 divided by that number. The reciprocal of 1/3 is 3/1 (or 3). Multiplying by the reciprocal is fundamentally what we're doing when we divide fractions.
This concept is crucial because it highlights the inverse relationship between multiplication and division. Dividing by a fraction is equivalent to multiplying by its reciprocal. This understanding extends beyond just fractions and applies to all numbers.
Working with Mixed Numbers: A Step-by-Step Guide
Let's extend our understanding to problems involving mixed numbers. Suppose we need to calculate 2 ½ divided by ⅓.
First, we need to convert the mixed number 2 ½ into an improper fraction. To do this, we multiply the whole number (2) by the denominator (2), add the numerator (1), and place the result over the original denominator:
(2 × 2 + 1) / 2 = 5/2
Now, we can apply the KCF method:
5/2 ÷ 1/3 becomes 5/2 × 3/1
Multiplying the numerators and denominators:
(5 × 3) / (2 × 1) = 15/2
Finally, we convert the improper fraction 15/2 back into a mixed number:
15/2 = 7 ½
Therefore, 2 ½ divided by ⅓ equals 7 ½.
Real-World Applications: Putting It All Together
Understanding fraction division is not just an academic exercise; it has many practical applications in daily life:
-
Cooking and Baking: Recipes often require dividing ingredients by fractions. For example, if a recipe calls for 1/3 cup of sugar but you want to make half the recipe, you need to divide 1/3 by 2.
-
Sewing and Crafting: Cutting fabric or other materials to precise measurements often involves fractional calculations.
-
Construction and Engineering: Precise measurements and calculations using fractions are essential in various construction and engineering projects.
-
Finance and Budgeting: Managing finances and budgets often involves working with fractions and percentages, which are closely related.
-
Data Analysis: Analyzing datasets and interpreting proportions often requires an understanding of fraction division.
Troubleshooting Common Mistakes
When working with fraction division, several common mistakes can occur:
-
Forgetting to flip the divisor: This is perhaps the most common error. Remember the KCF rule: Keep, Change, Flip.
-
Incorrect conversion of mixed numbers: Ensure you correctly convert mixed numbers into improper fractions before applying the KCF method.
-
Errors in multiplication: Double-check your multiplication of numerators and denominators to avoid simple calculation errors.
-
Failing to simplify the result: Always simplify your final answer to its lowest terms.
Advanced Concepts: Extending Your Knowledge
While the KCF method and the visual approach are sufficient for many applications, understanding the underlying mathematical principles can further enhance your grasp of fraction division. This includes exploring the concept of multiplicative inverses, working with complex fractions, and exploring different mathematical notations for division.
Conclusion: Mastering Fraction Division
Mastering fraction division is a crucial skill in mathematics with widespread applications in various fields. By understanding the "Keep, Change, Flip" method, visualizing the division process, and practicing regularly, you can confidently tackle problems involving fractions and mixed numbers. Remember to check for common mistakes and to always simplify your answers. With consistent practice and a deeper understanding of the underlying concepts, you'll be well-equipped to handle any fraction division challenge you encounter. The seemingly simple question "What is 2 divided by 1/3?" opens a door to a deeper understanding of mathematics and its practical applications in the real world.
Latest Posts
Latest Posts
-
Rational Functions X And Y Intercepts
Apr 07, 2025
-
Examples Of Right Angles In Real Life
Apr 07, 2025
-
What Is The Square Root Of 93
Apr 07, 2025
-
Common Denominator For 9 And 7
Apr 07, 2025
-
Square Root Of 1 To 20
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 Divided By 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.