What Is The Gcf Of 48 And 54
News Co
Apr 02, 2025 · 6 min read
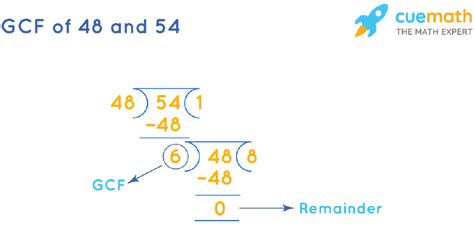
Table of Contents
What is the GCF of 48 and 54? A Deep Dive into Greatest Common Factor
Finding the greatest common factor (GCF) of two numbers might seem like a simple arithmetic task, but understanding the underlying principles and various methods for calculating it opens doors to a deeper appreciation of number theory and its applications in various fields. This comprehensive guide will explore the concept of GCF, specifically focusing on finding the GCF of 48 and 54, using multiple approaches. We will delve into the theoretical foundation, practical applications, and even touch upon the historical context of this fundamental mathematical concept.
Understanding Greatest Common Factor (GCF)
The greatest common factor (GCF), also known as the greatest common divisor (GCD), is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that can perfectly divide both numbers. For instance, if we consider the numbers 12 and 18, the factors of 12 are 1, 2, 3, 4, 6, and 12, while the factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors are 1, 2, 3, and 6. The greatest among these is 6, making 6 the GCF of 12 and 18.
This seemingly basic concept is crucial in various mathematical operations and has significant practical applications, as we'll see later.
Methods for Finding the GCF of 48 and 54
Several methods can be employed to determine the GCF of 48 and 54. Let's explore the most common ones:
1. Listing Factors
This method involves listing all the factors of each number and identifying the largest common factor.
- Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
- Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
Comparing the two lists, we find the common factors: 1, 2, 3, and 6. The greatest among these is 6. Therefore, the GCF of 48 and 54 is 6. This method is straightforward for smaller numbers but can become cumbersome for larger numbers with numerous factors.
2. Prime Factorization
This method uses the prime factorization of each number to find the GCF. Prime factorization involves expressing a number as a product of its prime factors.
- Prime factorization of 48: 2 x 2 x 2 x 2 x 3 = 2⁴ x 3
- Prime factorization of 54: 2 x 3 x 3 x 3 = 2 x 3³
To find the GCF, we identify the common prime factors and multiply them together, using the lowest power of each common factor. Both 48 and 54 share a common factor of 2 and a common factor of 3. The lowest power of 2 is 2¹ and the lowest power of 3 is 3¹. Therefore, the GCF is 2¹ x 3¹ = 6. This method is more efficient for larger numbers, especially when dealing with numbers that have many factors.
3. Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially large ones. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 48 and 54:
- 54 = 48 x 1 + 6 (We subtract 48 from 54, leaving a remainder of 6)
- 48 = 6 x 8 + 0 (We divide 48 by 6, leaving a remainder of 0)
The last non-zero remainder is 6, which is the GCF of 48 and 54. This method is highly efficient and avoids the need for extensive factorization, making it ideal for large numbers.
Applications of GCF
The GCF has numerous applications across diverse fields:
-
Simplifying Fractions: Finding the GCF helps in simplifying fractions to their lowest terms. For example, the fraction 48/54 can be simplified to 8/9 by dividing both the numerator and denominator by their GCF, which is 6.
-
Solving Word Problems: Many word problems in mathematics involve finding the GCF to determine the optimal solution. For example, imagine you have 48 red marbles and 54 blue marbles, and you want to divide them into identical groups with the maximum number of marbles in each group. The GCF (6) represents the maximum number of groups you can make, with each group containing 8 red and 9 blue marbles.
-
Geometry: GCF plays a significant role in geometry, particularly in problems related to area and perimeter calculations. Finding the dimensions of the largest possible square tile that can perfectly cover a rectangular area involves determining the GCF of the length and width of the rectangle.
-
Computer Science: The GCF is used in various algorithms in computer science, including cryptography and data compression. Efficient algorithms for finding the GCF are essential for optimizing these processes.
-
Music Theory: GCF finds application in music theory, especially in determining the intervals between notes. The GCF of two frequencies determines the simplest ratio between those frequencies.
Historical Context of GCF
The concept of the greatest common divisor has a rich history, dating back to ancient Greece. Euclid, in his seminal work Elements, presented the Euclidean algorithm, which remains one of the most efficient methods for calculating the GCF even today. This enduring algorithm highlights the timeless nature and practical significance of this fundamental mathematical concept. The development and refinement of methods for finding the GCF reflect the progress of mathematics throughout history, illustrating how seemingly simple concepts can have profound implications for more advanced mathematical concepts.
Beyond the Basics: Extending the Concept of GCF
While we focused on finding the GCF of two numbers, the concept can be extended to finding the GCF of three or more numbers. The methods outlined above, particularly prime factorization and the Euclidean algorithm (which can be adapted for more than two numbers), can be generalized to handle multiple numbers. Furthermore, the concept of GCF extends to more abstract mathematical structures, such as polynomials and ideals in abstract algebra. These advanced applications demonstrate the power and versatility of the seemingly simple concept of the greatest common factor.
Conclusion: The Importance of Understanding GCF
Understanding the greatest common factor is not merely an exercise in arithmetic; it's a foundational concept with widespread applications in various mathematical fields and practical scenarios. Mastering different methods for calculating the GCF, such as listing factors, prime factorization, and the Euclidean algorithm, equips individuals with a powerful tool for solving a wide range of problems, from simplifying fractions to tackling complex mathematical challenges in advanced fields. The enduring relevance of the GCF throughout history underscores its significance as a fundamental concept in mathematics, highlighting its continued importance in modern mathematics and beyond. The GCF of 48 and 54, while seemingly a small problem, serves as a gateway to understanding a much broader and profoundly important mathematical concept.
Latest Posts
Latest Posts
-
Mark The Integers On The Number Line
Apr 03, 2025
-
1 Cubic Meter Is How Many Cubic Centimeters
Apr 03, 2025
-
How To Convert A Mixed Fraction To A Whole Number
Apr 03, 2025
-
How To Change A Ratio To A Percent
Apr 03, 2025
-
How To Find Lateral Area Of Cone
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Gcf Of 48 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
