What Is The Lcm For 5 And 6
News Co
Apr 04, 2025 · 5 min read
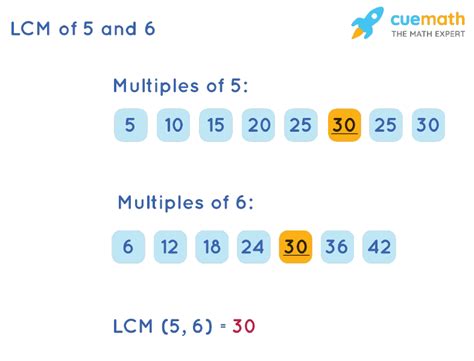
Table of Contents
What is the LCM for 5 and 6? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) is a fundamental concept in mathematics, crucial for various applications from simplifying fractions to solving complex equations. This article will comprehensively explore how to determine the LCM for 5 and 6, explaining the underlying principles and providing various methods to solve this and similar problems. We'll also delve into the broader context of LCMs and their significance in mathematics and beyond.
Understanding Least Common Multiples (LCM)
Before we tackle the specific problem of finding the LCM of 5 and 6, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is a multiple of all the integers. In simpler terms, it's the smallest number that can be divided evenly by all the given numbers without leaving a remainder.
For example, consider the numbers 2 and 3. The multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. The multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, and so on. The least common multiple is 6.
Methods for Finding the LCM of 5 and 6
There are several ways to determine the LCM of 5 and 6. Let's explore the most common and effective methods:
1. Listing Multiples
This is a straightforward method, particularly useful for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35...
- Multiples of 6: 6, 12, 18, 24, 30, 36...
The smallest number that appears in both lists is 30. Therefore, the LCM of 5 and 6 is 30.
2. Prime Factorization Method
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves finding the prime factorization of each number and then constructing the LCM from these prime factors.
- Prime factorization of 5: 5 (5 is a prime number)
- Prime factorization of 6: 2 x 3
To find the LCM using prime factorization, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2<sup>1</sup> = 2.
- The highest power of 3 is 3<sup>1</sup> = 3.
- The highest power of 5 is 5<sup>1</sup> = 5.
Multiplying these highest powers together, we get: 2 x 3 x 5 = 30. Therefore, the LCM of 5 and 6 is 30.
3. Using the Formula: LCM(a, b) = (|a x b|) / GCD(a, b)
This method utilizes the greatest common divisor (GCD) of the two numbers. The GCD is the largest number that divides both numbers evenly. We can use the Euclidean algorithm to find the GCD.
-
Finding the GCD of 5 and 6: Since 5 is a prime number and 6 is not divisible by 5, the GCD of 5 and 6 is 1.
-
Applying the formula: LCM(5, 6) = (|5 x 6|) / GCD(5, 6) = 30 / 1 = 30
This formula provides a concise and efficient way to calculate the LCM, especially when dealing with larger numbers where listing multiples becomes impractical.
Applications of LCM
The concept of LCM has numerous applications across various fields:
1. Fraction Addition and Subtraction
Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators. For instance, to add 1/5 and 1/6, we need to find the LCM of 5 and 6, which is 30. We then rewrite the fractions with a denominator of 30 before adding them.
2. Scheduling Problems
LCM is frequently used to solve scheduling problems. For example, if two buses depart from a station at different intervals, finding the LCM of their departure intervals helps determine when they will both depart simultaneously.
3. Cyclical Events
LCM is useful for problems involving cyclical events that repeat at different intervals. Consider two blinking lights that flash at different rates. The LCM of their flashing intervals determines when they will flash simultaneously.
4. Number Theory
LCM plays a significant role in number theory, particularly in problems related to modular arithmetic and divisibility.
5. Computer Science
In computer science, LCM finds applications in various algorithms and data structures, such as those dealing with synchronization and scheduling processes.
Beyond the Basics: LCM for More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. For the prime factorization method, we simply include all the prime factors from each number's factorization, taking the highest power of each. For the formula method, we can iteratively apply the formula to pairs of numbers, eventually obtaining the LCM of all the numbers.
For example, to find the LCM of 5, 6, and 10:
-
Prime factorization:
- 5 = 5
- 6 = 2 x 3
- 10 = 2 x 5
-
LCM: 2 x 3 x 5 = 30
Conclusion: Mastering LCM for Mathematical Success
Understanding and mastering the concept of LCM is crucial for anyone pursuing mathematical studies or working in fields that involve mathematical calculations. This article has provided a thorough explanation of the different methods for finding the LCM, particularly focusing on the LCM of 5 and 6. By understanding the underlying principles and applying the various methods, you can confidently tackle LCM problems of varying complexity and appreciate its wide-ranging applications in mathematics and beyond. Remember, practice is key to mastering this fundamental concept! Try finding the LCM of different number combinations to reinforce your understanding. The more you practice, the more intuitive this concept will become.
Latest Posts
Latest Posts
-
What Is 3 Out Of 5 As A Percentage
Apr 05, 2025
-
What Is The Common Multiple Of 3 And 5
Apr 05, 2025
-
30 Is What Percent Of 50
Apr 05, 2025
-
What Is 10 To The Power Of 8
Apr 05, 2025
-
What Is The Sum Of Interior Angles In A Hexagon
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm For 5 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
