Which Of The Following Correlations Is The Strongest
News Co
Apr 06, 2025 · 5 min read
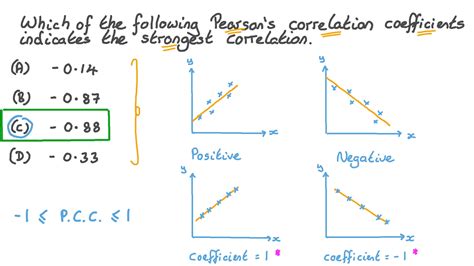
Table of Contents
Which of the following correlations is the strongest? Understanding Correlation Coefficients
Correlation is a fundamental concept in statistics that measures the strength and direction of a linear relationship between two variables. Understanding which correlation is strongest requires a grasp of the correlation coefficient, its interpretation, and the limitations of correlation analysis. This article delves deep into these concepts, providing a comprehensive guide to identifying the strongest correlation from a given set of values.
What is a Correlation Coefficient?
The correlation coefficient, most commonly represented by the letter r, is a numerical measure that quantifies the linear association between two variables. It ranges from -1 to +1, inclusive. The closer the absolute value of r is to 1, the stronger the linear relationship. The sign of r indicates the direction of the relationship:
- Positive correlation (+1): As one variable increases, the other tends to increase. This indicates a direct relationship.
- Negative correlation (-1): As one variable increases, the other tends to decrease. This indicates an inverse relationship.
- Zero correlation (0): There's no linear relationship between the variables. This doesn't necessarily mean there's no relationship at all; it simply means there's no linear relationship. A non-linear relationship might still exist.
Understanding the Strength of Correlation:
The strength of the correlation is determined by the absolute value of the correlation coefficient:
- |r| = 0.0 to 0.2: Very weak or no correlation.
- |r| = 0.2 to 0.4: Weak correlation.
- |r| = 0.4 to 0.6: Moderate correlation.
- |r| = 0.6 to 0.8: Strong correlation.
- |r| = 0.8 to 1.0: Very strong correlation.
Interpreting Correlation Coefficients: Examples
Let's illustrate with examples:
- r = 0.85: This indicates a very strong positive correlation. As one variable increases, the other increases significantly.
- r = -0.70: This indicates a strong negative correlation. As one variable increases, the other decreases substantially.
- r = 0.15: This suggests a very weak positive correlation. The relationship between the variables is barely noticeable.
- r = -0.30: This shows a weak negative correlation. The inverse relationship is not very pronounced.
- r = 0.98: This represents an extremely strong positive correlation, indicating a near-perfect linear relationship.
Important Considerations When Interpreting Correlations:
- Causation vs. Correlation: Correlation does not imply causation. Just because two variables are correlated doesn't mean one causes the other. There might be a third, unobserved variable influencing both.
- Outliers: Outliers can significantly influence the correlation coefficient. A single outlier can artificially inflate or deflate the value of r. It's crucial to identify and consider the impact of outliers.
- Linearity: The correlation coefficient measures only linear relationships. If the relationship between the variables is non-linear (e.g., curvilinear), the correlation coefficient might be misleadingly low or even close to zero, even if a strong relationship exists. Visual inspection of a scatter plot is always recommended.
- Sample Size: The reliability of the correlation coefficient increases with the sample size. A correlation calculated from a small sample might not be representative of the population.
Determining the Strongest Correlation from a Set of Values
To determine the strongest correlation from a set of correlation coefficients, simply compare the absolute values of the coefficients. The coefficient with the largest absolute value represents the strongest relationship.
Example:
Consider the following correlation coefficients:
- r₁ = 0.75
- r₂ = -0.82
- r₃ = 0.60
- r₄ = -0.25
To determine the strongest correlation:
- Find the absolute values: |r₁| = 0.75, |r₂| = 0.82, |r₃| = 0.60, |r₄| = 0.25
- Compare the absolute values: The largest absolute value is 0.82 (r₂).
Therefore, r₂ = -0.82 represents the strongest correlation among the given set. It indicates a strong negative linear relationship between the two variables.
Beyond Pearson's r: Other Correlation Measures
While Pearson's r is the most common correlation coefficient, it's not always the most appropriate measure. Other correlation measures exist, each designed for specific data types and relationship patterns:
- Spearman's rank correlation (ρ): This is a non-parametric measure used for ordinal data or when the relationship between variables is not linear. It assesses the monotonic relationship (whether the variables consistently increase or decrease together).
- Kendall's tau (τ): Another non-parametric measure, similar to Spearman's rank correlation, also suitable for ordinal data or non-linear relationships.
- Point-biserial correlation: Used when one variable is continuous and the other is dichotomous (binary).
- Phi coefficient: Used when both variables are dichotomous.
The choice of correlation coefficient depends heavily on the nature of your data and the type of relationship you're investigating. Always carefully consider the characteristics of your data before selecting a correlation measure.
Advanced Techniques and Considerations
Analyzing correlations effectively involves more than just calculating a single coefficient. Here are some advanced techniques and considerations:
- Partial Correlation: This technique helps to isolate the correlation between two variables while controlling for the influence of a third variable. It's useful when you suspect that a third variable is confounding the relationship between your variables of interest.
- Multiple Correlation: This extends the concept of correlation to analyze the relationship between one variable and multiple predictor variables.
- Canonical Correlation: Used when you have multiple variables in each of two sets and want to identify the relationships between these sets.
- Scatter Plots and Visualizations: Always visually inspect your data using scatter plots to understand the relationship between variables. This helps identify non-linear relationships, outliers, and other patterns that might not be captured by the correlation coefficient alone.
- Statistical Significance Testing: The correlation coefficient should be accompanied by a test of statistical significance (e.g., t-test) to determine whether the observed correlation is likely due to chance or reflects a real relationship in the population.
Conclusion: Mastering Correlation Analysis
Understanding correlation coefficients and their interpretation is vital for researchers and data analysts across various fields. The strength of a correlation is determined by the absolute value of the correlation coefficient, with values closer to 1 indicating stronger relationships. However, remember that correlation does not equal causation, and careful consideration of data characteristics, potential outliers, and the type of relationship is crucial for accurate interpretation. By mastering these concepts and utilizing advanced techniques when necessary, you can effectively analyze relationships between variables and draw meaningful conclusions from your data. Remember to always supplement your numerical analysis with visualizations to gain a comprehensive understanding of the patterns within your data. This comprehensive approach will lead to more robust and reliable findings in your research.
Latest Posts
Latest Posts
-
Examples Of Right Angles In Real Life
Apr 07, 2025
-
What Is The Square Root Of 93
Apr 07, 2025
-
Common Denominator For 9 And 7
Apr 07, 2025
-
Square Root Of 1 To 20
Apr 07, 2025
-
How To Write In Logarithmic Form
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Which Of The Following Correlations Is The Strongest . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.